Сферичні двокутники та трикутники. Сферичний надлишок. Сферична тригонометрія.
Будь-які дві прямі сферичної геометрії розбивають сферу на чотири області, кожна з яких називається сферичним двокутником. Двокутник є аналогом многокутника, а саме, це многокутник, який має дві сторони. Таких фігур на евклідовій площині не існує. Двокутник повністю визначається кутом між прямими (відрізки яких є його сторонами).
Має місце наступна формула для площі двокутника
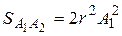 ,
,
де 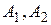 – вершини двокутника.
– вершини двокутника.
Три попарно різні великі кола сфери розбивають її на 8 областей, кожна з яких називається сферичним трикутникам. Будемо розглядати лише ті з них, які мають менші за  довжини сторін і менші за
довжини сторін і менші за 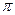 величини кутів (ейлерові трикутники).
величини кутів (ейлерові трикутники).
Нехай 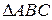 – ейлерів. Якщо
– ейлерів. Якщо 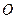 – центр сфери, то геометрію тригранного кута
– центр сфери, то геометрію тригранного кута 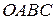 доцільно використати для вивчення геометрії сферичного трикутника. Наведемо деякі формули цієї геометрії.
доцільно використати для вивчення геометрії сферичного трикутника. Наведемо деякі формули цієї геометрії.
Позначимо 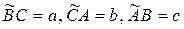 . Пари точок
. Пари точок 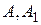 ,
, 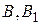 ,
, 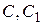 - діаметрально протилежні. Між площами сфери, сферичного трикутника і сферичних двокутників можна встановити такий зв'язок:
- діаметрально протилежні. Між площами сфери, сферичного трикутника і сферичних двокутників можна встановити такий зв'язок:
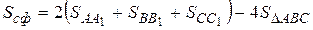 ,
,
тоді формула площі сферичного трикутника має вигляд
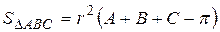 ,
,
звідки випливає, що в сферичній геометрії сума кутів трикутника більша за 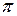 .
.
Далі, для зручності, позначимо 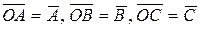 . Для сторін
. Для сторін 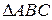 маємо
маємо
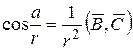 ,
, 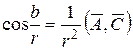 ,
, 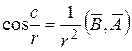 ,
,
а для кутів –
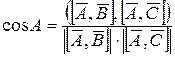 ,
, 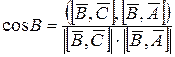 ,
, 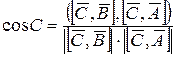 .
.
Для елементів сферичного трикутника виконується перша теорема косинусів
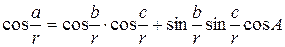 ,
,
друга теорема косинусів
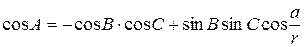 ,
,
теорема синусів
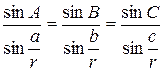 .
.
Для прямокутного сферичного трикутника формула з першої теореми косинусів отримаємо аналог теореми Піфагора у вигляді
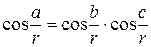
Дата добавления: 2016-12-08; просмотров: 1470;
