Приклади розв’язання задач

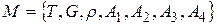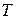Задача 1. Дано математичну структуру , де – множина точок, 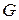– множина прямих, 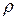– відношення приналежності таке, що виконуються аксіоми:

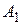: для будь-яких двох різних точок існує пряма, що містить кожну з них.

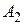: для будь-яких двох різних точок існує не більше однієї прямої, що містить кожну з них.

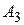: на кожній прямій існує принаймні дві точки.

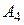: існує трійка точок, що не належать одній прямій.

Дослідити систему аксіом на несуперечність, на незалежність і повноту.

Розв’язання.Для перевірки системи аксіом на несуперечність побудуємо модель цієї системи. Визначимо основні поняття даної структури: "точка" – будь-яка з трьох точок 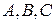евклідової площини, "пряма" – будь-яка з невпорядкованих пар 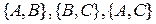, "належати" – як елемент множині 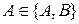, 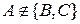. Перевіримо, чи виконуються аксіоми.

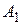: Візьмемо, наприклад, точки 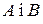, для них існує пряма 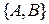, якій вони належать. Для інших двох пар точок висновок такий самий.

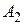: Для кожної з трьох можливих пар точок існує єдина пряма, якій вони належать.

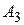: На кожній з трьох означених прямих існують по дві точки.

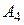:Існують три точки 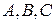, що одночасно не належать жодній із означених прямих .

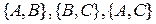Таким чином, побудовано модель цієї системи аксіом, а значить вона є несуперечливою.

Перевіримо аксіому 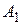на незалежність. Розглянемо систему 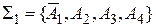, де аксіома 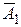: «Існує принаймні дві різні точки, для яких не існує прямої, якій обидві ці точки належать» є запереченням аксіоми 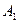. Треба перевірити систему 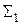на несуперечливість. Розглянемо наступну модель цієї системи. "Точкою" назвемо будь-яку з трьох точок 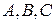евклідової площини, "прямою" – будь-яку з невпорядкованих пар 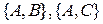, "належати" – в теоретико-множинному сенсі (елемент належить множині). Перевіримо, чи виконуються аксіоми.

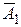: Для точок 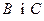не існує прямої, якій обидві ці точки належать.

Очевидно, що і аксіоми 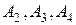виконуються, отже система 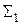–несуперечлива. Значить аксіома 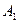не залежить від аксіом .

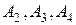Далі перевіримо незалежність аксіоми 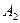. Розглянемо систему 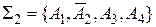, де 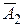: «Існують принаймні дві різних точки, для яких існують принаймні дві різні прямі, що містять ці точки». Визначимо поняття: "точка" – будь-яка з трьох точок 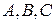евклідової площини, "пряма" – будь-яка з впорядкованих пар 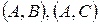, , 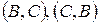"належати" – як елемент множині. Легко бачити, що аксіоми 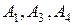виконуються. Для доведення аксіоми 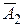розглянемо точки 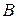та 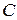. Для них існують дві різні прям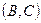і і 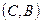, що їх містять. Отже, система 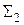– несуперечлива, а значить,. аксіома 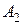не залежить від аксіом .

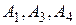Аналогічно доводиться незалежність аксіом 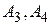(самостійно). Доведено незалежність заданої системи аксіом.

Дана система аксіом не буде повною, бо існують не ізоморфні моделі цієї системи. Наприклад, модель 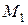, в якій три точки 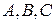та три прямі 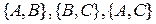та модель 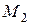, в якій чотири точки 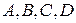та шість прямих 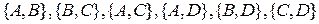пов’язані відношенням приналежності в зазначеному вище сенсі, не ізоморфні.

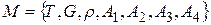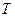Задача 2.Дано математичну структуру , де – множина точок, 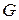– множина прямих, 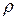– відношення приналежності таке, що виконуються аксіоми:

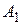: для будь-яких двох різних точок існує єдина пряма, що містить кожну з них.

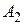: на кожній прямій існує принаймні дві точки.

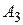: існує трійка точок, що не належать одній прямій.

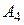: через будь-яку точку, що не належить даній прямій, проходить єдина пряма, що не перетинає дану пряму.

Дослідити систему аксіом на несуперечність, аксіому 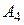на незалежність.

Розв’язання.Визначимо поняття: "точка" – будь-яка з чотирьох точок 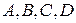евклідової площини, "пряма" – будь-яка з невпорядкованих пар 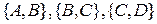, , 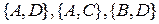"належати" – як елемент множині: 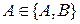, "паралельні прямі" – ті, що не мають спільних точок із точок .

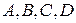Дослідження систему аксіом на несуперечністьпроводиться аналогічно задачі 1. Очевидно, що аксіоми 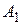, , 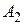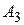виконуються. Доведемо аксіому 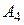. Нехай 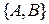– дана пряма, а 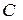– точка, що їй не належить. Тоді серед прямих 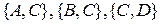, що містять точку 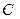, лише одна пряма 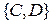паралельна прямій 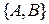. Так само для інших п’яти прямих.

Для перевірки аксіоми 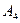на незалежність треба дослідити систему аксіом 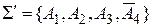на несуперечливість.

Задача 3. Довести, що система аксіом метричної структури залежна.

Доведення.Нагадаємо означення метрики: Метрикою (або відстанню) на довільній непорожній множині 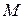називається така дійсна функція 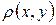, визначена для всіх 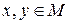, яка задовольняє наступним аксіомам:

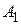.Для будь-яких 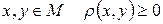(аксіома невід’ємності);

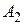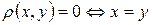. (аксіома тотожності);

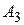.Для будь-яких 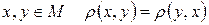(аксіома симетрії);

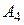.Для будь-яких 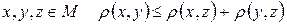(нерівність трикутника).

Доведемо, що досить прийняти лише аксіоми 2 і 4, а аксіоми 1 і 3 отримати як наслідки. Запишемо аксіому 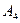для набору 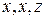, отримаємо

,

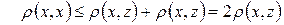звідки, з урахуванням аксіоми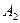

,

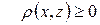тобто виконується аксіома .

Далі, для набору аксіома прийме вигляд

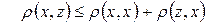, або ,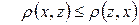

а для набору –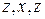

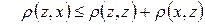, або .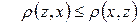

Отже, 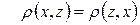, тобто аксіома 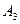теж доведена.

Задача 4. Довести незалежність аксіоми 4.4 системи аксіом Вейля.

Розв’язання.Для доведення незалежності аксіоми 4.4 від інших аксіом системи аксіом Вейля розглянемо систему 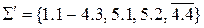, де

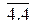: «Існують принаймні два таких ненульових вектора 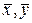, що ».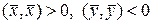

Побудуємо модель. Основні поняття «точка», «вектор», «сума векторів», «добуток вектора на число» та «відкладання вектора від точки» означимо так само як і при побудові арифметичної моделі. Скалярний добуток векторів 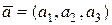та 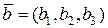означимо формулою

.

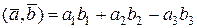Очевидно, що аксіоми 4.1, 4.2, 4.3 виконуються. Для перевірки аксіоми 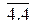розглянемо вектори 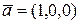та 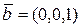і знайдемо їх скалярні квадрати:

, .

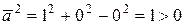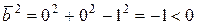Таким чином, система 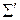– несуперечлива, отже , аксіома 4.4 не залежить від інших аксіом системи Вейля.

Задача 5. Довести, не використовуючи комутативність додавання векторів, наступні твердження:

1). .

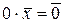2). .

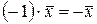3). .

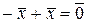4). .

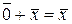5). .

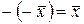6). .

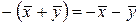Розв’язання.Над знаками «=» будемо інколи записувати номер аксіоми або доведеного твердження

1). 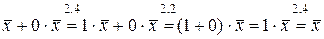. З аксіоми 1.3 випливає, що .

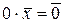2). 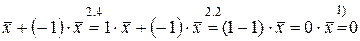, отже .

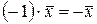3). .

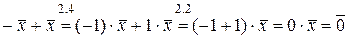4). .

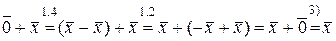5). .

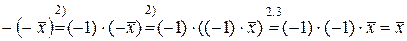6). .

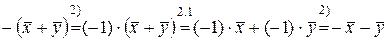Задача 6.Довести залежність аксіоми 1.1: 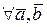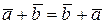комутативності суми векторів від аксіом перших двох груп аксіоматики Вейля.

Розв’язання.Почнемо з лівої частини рівності і застосуємо аксіоми та доведені в попередній задачі властивостями, записуючи їх номери над знаками рівності, отримаємо

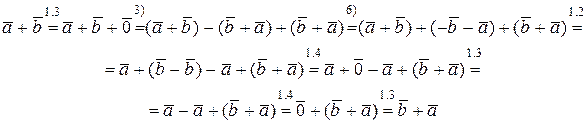
Висновок. Система аксіом Вейля залежна.

Задачі для самостійного розв’язання.

1.Точкою назвемо будь-яку точку площини, окрім однієї точки (точки О), прямою назвемо будь-яку пряму цієї площини, що проходить через точку О, або будь-яке коло, що проходить через точку О. Відношення «належати» розуміємо в теоретико-множинному сенсі. Дві прямі одного типу будемо називати паралельними, якщо вони не перетинаються. Показати, що наведений опис дає модель системи аксіом із задачі 2.

2. Які з наступних тверджень справедливі для вказаних множин точок і прямих і відношення належності:

1) «Точка» - довільна внутрішня точка круга на евклідовій площині, «пряма» - довільна хорда цього круга (без кінців), «належить», «перетинаються» - в теоретико-множинному сенсі.

2) «Точка» - довільне коло радіуса 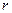на евклідовій площині, «пряма» - довільна пара паралельних прямих, евклідова відстань між якими дорівнює 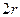, «точка належить прямій» - коло дотикається до пари паралельних прямих, «перетинаються» - в теоретико-множинному сенсі

3) «Точка» - довільна сфера радіуса 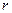в евклідовому просторі, «пряма» - довільний круговий циліндр радіуса 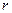, «точка належить прямій» - сфера дотикається до поверхні циліндра, «перетинаються» - в теоретико-множинному сенсі.

4) «Точка» - довільна пряма зв’язки прямих з центром О в евклідовому просторі, «пряма» - довільна площина цієї зв’язки, «точка належить прямій» - пряма зв’язки належить площині зв’язки, «перетинаються» - в теоретико-множинному сенсі. (зв’язка – множина прямих і площин, що проходять через одну точку).

Твердження:

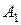: для будь-яких двох різних точок існує єдина пряма, якій належить кожна з точок.

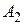: для будь-яких двох різних прямих існує єдина точка, яка належить кожній з прямих.

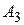: кожній прямою належать принаймні дві точки.

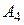: існує трійка точок, що не належать одній прямій.

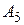: через будь-яку точку, що не належить цій прямій, проходить єдина пряма, що не перетинає цю пряму.

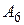: через будь-яку точку, що не належить цій прямій, проходить дві прямі, що не перетинають цю пряму.

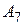: існує чотири точки, ніякі три з яких не належать одній прямій