Приклади розв’язання задач

Користуючись аксіомами 1.1-1.3 аксіоматики Гільберта довести твердження.

Задача 1. Будь-які дві різні прямі мають не більше однієї спільної точки.

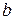Розв’язання.Скористаємось методом від супротивного. Нехай і – різні прямі, які мають дві спільні точки: , тобто та 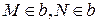. Тоді через дві різні точки 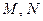проходить дві прямі, що суперечить аксіомі 1.2.

Задача 2.(Th. 17 bis з додатку Г) В рівнобедреному трикутнику медіана основи є висотою та бісектрисою кута при вершині.

Доведення. Розглянемо рівнобедрений трикутник 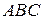, в якому проведена медіана 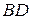. За умовою задачі 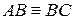, 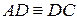. За теоремою 17 , а, з теореми 14 випливає, що 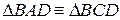. З рівності цих трикутників випливає, що 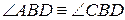, тобто 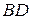– бісектриса 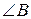. Також з рівності 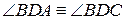суміжних кутів випливає, що кожен з них прямий, отже 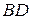– висота.

Задача 3.(Th. 25)Довести, що з будь-якої точки можна опустити на пряму один і тільки один перпендикуляр.

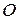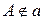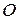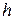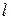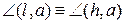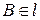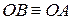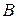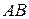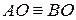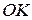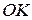Доведення. На прямій візьмемо точку . Через точку та точку проведемо пряму . За аксіомою 3.4. існує єдина пряма така, що . За аксіомою 3.1. існує єдина точка : . Оскільки точки і лежать в різних півплощинах, то за теоремою 10 прямі та перетинаються. Розглянемо трикутник . За побудовою , – бісектриса . Отже, – висота (за теоремою 17 bis).