Приклади розв’язання задач
Задача 1. Довести, що 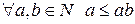 , вважаючи, що властивості числових нерівностей вже доведено.
, вважаючи, що властивості числових нерівностей вже доведено.
Розв’язання.Розглянемо очевидну для будь-якого натурального числа нерівність 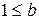 . За властивістю монотонності відносно множення для довільного
. За властивістю монотонності відносно множення для довільного 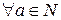 отримаємо нерівність
отримаємо нерівність 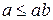 .
.
Задача 2. Теорема (Архімеда). 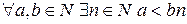 .
.
Доведення.Зрозуміло, що треба розглянути лише випадок 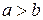 . За означенням відношення порівняння натуральних чисел в цьому випадку існує натуральне число
. За означенням відношення порівняння натуральних чисел в цьому випадку існує натуральне число 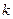 таке, що
таке, що 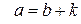 . Візьмемо
. Візьмемо 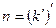 і застосуємо означення множення. Тоді
і застосуємо означення множення. Тоді 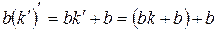 . Отже, треба порівняти числа
. Отже, треба порівняти числа 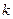 і
і 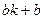 . За попередньою теоремою
. За попередньою теоремою 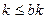 , а значить при будь-якому натуральному
, а значить при будь-якому натуральному 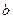 отримаємо
отримаємо 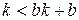 , звідки випливає нерівність, що доводиться.
, звідки випливає нерівність, що доводиться.
Задача 3. Довести, що 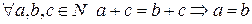 .
.
Доведення.Застосуємо принцип індукції по 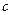 . При
. При 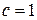 одержимо
одержимо
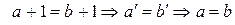 .
.
Припустимо, що для натурального 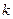 вірна імплікація
вірна імплікація
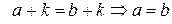 .
.
Для 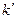 отримаємо
отримаємо 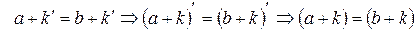 . За індуктивним припущенням маємо наслідок
. За індуктивним припущенням маємо наслідок 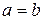 . Отже,
. Отже, 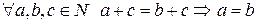 .
.
Задача 4. Показати, що між довільними двома різними раціональними числами існує принаймні одне раціональне число.
Вказівка.Розгляньте півсуму даних чисел.
Задача 5. Показати, що в множині раціональних чисел не існує такого перерізу, що в класі А є найбільший, а в класі В є найменший елемент.
Доведення.Нехай а - найбільший в А, в - найменший в В. Тоді а<в. Існує раціональне с таке, що а<с<в. Оскільки c>a, то с не належить до класу А, оскільки c<в, то с не належить до В. Отримали протиріччя з означенням перерізу.
Задача 6.Довести властивість різниці: 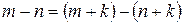 .
.
Розв’язання.Нехай 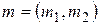 ,
, 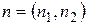 ,
, 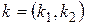 . Тоді
. Тоді
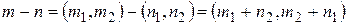 ,
,
і
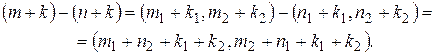
Цілі числа в правих частинах останніх двох рівностей належать одному класу, або, інакше, рівні між собою.
Задачі для самостійного розв’язання.
1. Впорядкувати цілі числа
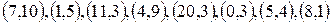 .
.
2. Впорядкувати раціональні числа:
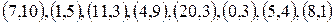 .
.
З. Порівняти цілі числа і знайти їх суму та різницю: 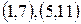 .
.
4. Порівняти раціональні числа і знайти їх суму та різницю: 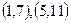
5. Довести властивості різниці
1). 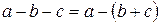 ,
,
2). 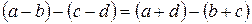 ,
,
3). 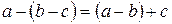 .
.
6. Довести рівності 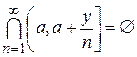 ,
, 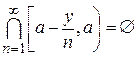 .
.
7. На множині 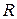 операція додавання визначена наступним чином:
операція додавання визначена наступним чином: 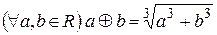 . Операція множення звичайна. Перевірити, чи для цих операцій виконуються аксіоми системи дійсних чисел. Виразити похідну, задану формулою
. Операція множення звичайна. Перевірити, чи для цих операцій виконуються аксіоми системи дійсних чисел. Виразити похідну, задану формулою 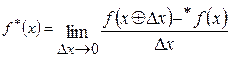 , через звичайну похідну.
, через звичайну похідну.
8. Довести наслідки з аксіом множини дійсних чисел:
1) для будь-яких 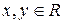 має місце лише одне із співвідношень:
має місце лише одне із співвідношень: 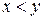 ,
, 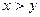 ,
, 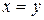 .
.
2) для будь-яких 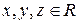 виконується імплікація:
виконується імплікація: 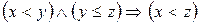 .
.
3) для будь-якого 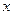 виконується імплікація
виконується імплікація 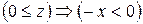 .
.
4) 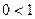 .
.
Дата добавления: 2016-12-08; просмотров: 976;
