Тема 3: Системи аксіом евклідової геометрії. Еквівалентність систем аксіом Вейля та Гільберта
Мета:Порівняти аксіоматичні теорії евклідової геометрії, побудовані на базі систем аксіом Вейля та Гільберта.
Методичні рекомендації.Математична структура «евклідова геометрія»може бути побудована на базі різних систем аксіом. Порівняння різних аксіоматичних теорій евклідової геометрії є важливим для розуміння аксіоматичного методу як засобу для її обґрунтування. Доведення еквівалентності систем Вейля і Гільберта підкреслює той факт, що такі різні системи аксіом дозволяють побудувати теорію однієї математичної структури.
Приклади розв’язання задач
Розв’язати задачі в аксіоматичній теорії Вейля:
Задача 1.Довести, що середня лінія трапеції паралельна її основам та дорівнює їх півсумі.
Розв’язання.
 Розглянемо трапецію
Розглянемо трапецію 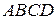 з основами
з основами 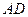 і
і 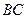 та середньою лінією
та середньою лінією 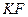 . Доведемо, що
. Доведемо, що
1. 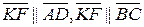
2. 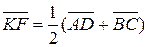 .
.
Користуючись аксіомами 1.3, 1.4, 2.3, 5.2, можна записати
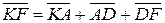 та
та  . Або
. Або 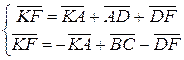 . Сума отриманих векторних рівностей дає векторну рівність
. Сума отриманих векторних рівностей дає векторну рівність 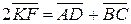 . З визначення трапеції випливає, що
. З визначення трапеції випливає, що 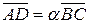 , тобто
, тобто  або
або 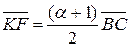 . З цього випливає, що
. З цього випливає, що 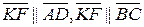 .
.
Доведемо другу властивість середньої лінії трапеції. Для цього треба скористатись такою властивістю векторів:
якщо 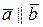 , то
, то 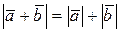 . Оскільки
. Оскільки 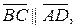 то з векторної рівності
то з векторної рівності 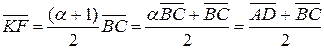 отримаємо скалярну рівність
отримаємо скалярну рівність
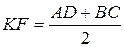 ,
,
яку і требі було довести.
Задача 2. Довести, що діагоналі прямокутника рівні між собою.
 Доведення.Розглянемо прямокутник
Доведення.Розглянемо прямокутник 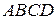 з діагоналями
з діагоналями 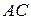 та
та 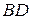 . Доведемо, що
. Доведемо, що 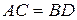 .
.
Виразимо вектори діагоналей через вектори сторін прямокутника за аксіомою 5.2:
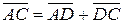 та
та 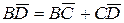 .
.
Знайдемо скалярні квадрати обох векторів, отримаємо
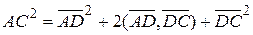 та
та 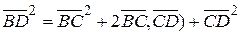 .
.
Оскільки 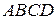 – прямокутник, то
– прямокутник, то 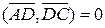 ,
, 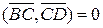 ,
, 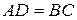 та
та 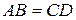 . З цього випливає, що знайдені скалярні квадрати векторів рівні, а значить і довжини цих векторів рівні, тобто
. З цього випливає, що знайдені скалярні квадрати векторів рівні, а значить і довжини цих векторів рівні, тобто 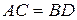 . Доведено.
. Доведено.
Задача 3. Довести, що медіани трикутника перетинаються в одній точці.
 Доведення.Спочатку визначимо положення точки, що ділить відрізок в даному відношенні.
Доведення.Спочатку визначимо положення точки, що ділить відрізок в даному відношенні.
Умова ділення рівносильна векторній рівності  ,
, 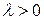 . За аксіомою 5.2
. За аксіомою 5.2 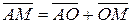 ,
, 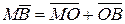 , і рівність набуває вигляду
, і рівність набуває вигляду  або
або  , звідки
, звідки 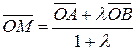 .
.
Далі розглянемо трикутник 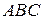 . Проведемо в ньому медіани
. Проведемо в ньому медіани 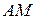 ,
,  та
та 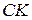 . Доведемо, що всі вони перетинаються в одній точці.
. Доведемо, що всі вони перетинаються в одній точці.
 Нехай медіани
Нехай медіани 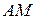 та
та  перетинаються в точці О. Запишемо векторне співвідношення для третьої медіани
перетинаються в точці О. Запишемо векторне співвідношення для третьої медіани 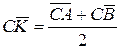 .
.  Нехай
Нехай 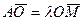 , тоді
, тоді 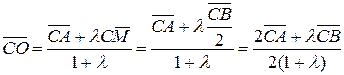 . Аналогічно, якщо
. Аналогічно, якщо 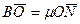 , тоді
, тоді 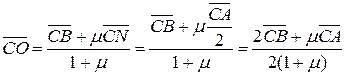 . За теоремою про однозначність розкладу вектора по одним і тим же лінійно незалежним векторам отримаємо
. За теоремою про однозначність розкладу вектора по одним і тим же лінійно незалежним векторам отримаємо 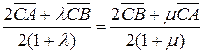 , що рівносильне системі рівнянь відносно невідомих
, що рівносильне системі рівнянь відносно невідомих 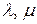 , з якої
, з якої 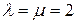 . Таким чином,
. Таким чином, 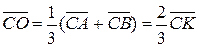 . Остання векторна рівність дає висновок про належність точки О медіані
. Остання векторна рівність дає висновок про належність точки О медіані 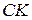 .
.
Задача 4.Користуючись системою аксіом Вейля евклідової планіметрії довести, що для будь-яких трьох точок 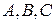 справедлива нерівність трикутника:
справедлива нерівність трикутника: 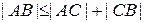 .
.
Доведення. За аксіомою 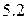 для будь-яких точок
для будь-яких точок 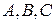 вірна рівність
вірна рівність 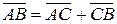 . Тоді
. Тоді 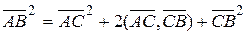 . За нерівністю Коші-Буняковського для будь-яких векторів маємо
. За нерівністю Коші-Буняковського для будь-яких векторів маємо 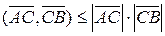 . Отже,
. Отже, 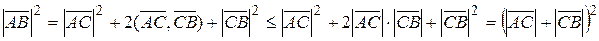 , звідки і отримаємо
, звідки і отримаємо 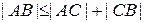 .
.
Дата добавления: 2016-12-08; просмотров: 1098;
