Задача 7.(Th. 34)Довести, що кожна сторона трикутника менша суми та більша різниці інших його сторін.

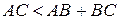Доведення. Розглянемо трикутник . Доведемо, що та 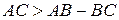. З аксіоми 3.1 випливає, що існує єдина точка така, що 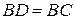. Утворився рівнобедрений трикутник 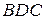, в якому 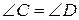(за теоремою 17). Очевидно, що 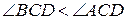, тоді 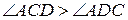, звідки .

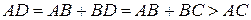Задача 8.Зробити логічний аналіз означення поняття «паралелограм».

Розв’язання.Означення поняття паралелограм відноситься до типу означень «через найближчий рід і видову ознаку». Найближчим родом для поняття паралелограм є поняття чотирикутника, для поняття чотирикутник – многокутник і так далі, поки не дійдемо до неозначуваних понять «точка», «пряма», «лежати між» (дивись блок-схему).

Задачі для самостійної роботи.

Користуючись аксіомами перших трьох груп аксіом системи Гільберта, довести твердження:

1. Перша ознака рівності трикутників.

2. Кути при основі рівнобедреного трикутника рівні.

3. Усі прямі кути конгруентні між собою.

4. Кожен кут можна розділити навпіл, причому єдиним чином.

5. У будь-якому трикутнику принаймні два кути є гострими.

6. З кожної точки на прямій можна відновити до цієї прямої єдиний перпендикуляр.