Приклади розв’язання задач

Задача 1.Довести, що при перетині двох паралельних прямих третьою утворюються рівні навхрест розташовані кути.

Доведення. Сформульоване твердження в «Началах» Евкліда було теоремою 29 і це була перша теорема, в доведенні якої використовувався 5 постулат.

Паралельні прямі а і 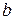утворюють з їх січною 2 пари навхрест розташованих кутів, які позначимо 1 і 4, 2 і 3, а пари 1 і 2, 3 і 4 – пари односторонніх кутів, 1 і 3 – суміжні. Припустимо, що кут 1 не дорівнює куту 4, і для визначеності, нехай кут 1 більше за кут 4. Тоді сума кутів 3 і 4 менша за розгорнутий кут, а отже за 5 постулатом прямі а і 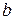перетинаються. Отримане протиріччя доводить теорему.

Задача 2. Довести, що сума внутрішніх кутів трикутника дорівнює сумі двох прямих кутів.

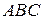Доведення. Розглянемо трикутник . Проведемо пряму 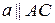. З теореми 47 випливає, що 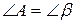, 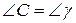. Оскільки кути 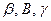утворюють розгорнутий кут, то для суми кутів трикутника отримаємо 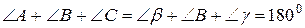, що і треба було довести.

Довести еквівалентність п’ятого постулату та наступних тверджень:

Задача 3. Перпендикуляр і похила, проведені в одній площині до даної прямої, перетинаються.

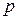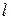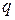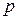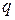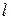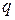Доведення. 1) Покажемо, що це твердження випливає з п’ятого постулату. До прямої в точці проведемо перпендикуляр та похилу . Проведемо ще один перпендикуляр до прямої . За теоремою 45 і паралельні. Приспустимо, що і не перетинаються, тоді отримаємо протиріччя з аксіомою паралельності, яка еквівалентна п’ятому постулату.

2) Покажемо, що з твердження випливає аксіома паралельності. Розглянемо пучок прямих, що проходять через точку . В цьому пучку є єдина пряма, яка не є похилою, це пряма 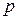, перпендикулярна до прямої . За умовою кожна похила перетинає перпендикуляр 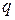. Отже, через точку , яка не належить прямій 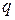, проходить єдина пряма 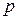, яка не перетинає пряму 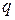, тобто виконується аксіома паралельності.

Задача 4.Навколо кожного трикутника можна описати коло.

Доведення.1) Покажемо, що з аксіоми паралельності випливає твердження: Два серединних перпендикуляра до двох сторін трикутника завжди перетинаються.

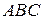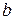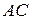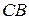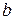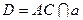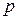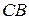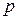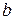В трикутнику проведемо серединні перпендикуляри і до сторін і відповідно. Припустимо, що прямі і не перетинаються, тобто паралельні. Проведемо через точку пряму , перпендикулярну до . За теоремою 45 прямі і не перетинаються. Таким чином, через точку 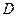проходить дві різні прямі, які не перетинають 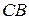. Отримали протиріччя з аксіомою паралельності, значить наше припущення невірне.

Точка перетину серединних перпендикулярів і є центром описаного навколо трикутника кола.

2) Тепер покажемо, що з цього твердження випливає аксіома паралельності.

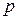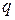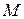До прямої проведемо перпендикуляр та похилу . На прямій візьмемо точку , симетричну їй відносно прямої 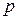точку 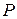та симетричну їй відносно прямої 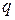точку 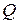. Очевидно, що точки 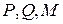не належать одній прямій, тобто утворюють трикутник. За побудовою 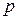і 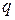– серединні перпендикуляри до двох сторін цього трикутника. За умовою, навколо 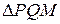можна описати коло, а значить 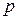і 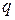, а значить перпендикуляр і похила до однієї прямої перетинаються. В попередній задачі було доведено, що з цього факту випливає аксіома паралельності.

Задача 5.Сума внутрішніх кутів в кожному трикутнику одна і та сама.

Доведення. 1) В задачі 2 цієї теми показано, що з аксіоми паралельності випливає, що в кожному трикутнику сума внутрішніх кутів дорівнює двом прямим кутам, тобто одна і та сама.

2) Покажемо як з твердження випливає п’ятий постулат. В трикутнику 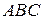позначимо кути так, як показано на рисунку. Можна записати такі рівності:

,

,

,

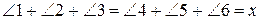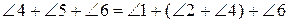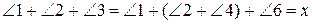Запишемо вирази 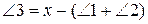та 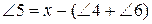. Знайдемо суми правих та лівих частин двох останніх рівностей

,

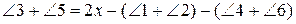звідки

.

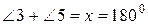Твердження про те, що в кожному трикутнику сума внутрішніх кутів дорівнює 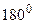, еквівалентне п’ятому постулату.