Задачі для самостійного розв’язання.

Довести наступні твердження в геометрії Лобачевського:

1. Сума внутрішніх кутів будь-якого трикутника менша .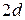

2. Сума внутрішніх кутів будь-якого опуклого чотирикутника менша за .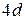

3. Для будь-яких двох паралельних прямих існує і тільки одна пряма, яка перпендикулярна одній із двох даних прямих і паралельна другій.

4. Будь-які дві паралельні прямі мають вісь симетрії.

5. Сума внутрішніх кутів трикутника не є постійною.

6. Множина точок площини, рівновіддалених від даної прямої є кривою (яка називається еквідистантою).

7. Ортогональна проекція однієї із сторін гострого кута на другу сторону є пів інтервалом.

8. Катет прямокутного трикутника, який є протилежним до кута з величиною 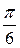, менший за половину гіпотенузи.

9. Яким повинен бути гострий кут, щоб ортогональна проекція однієї із його сторін на іншу сторону була не більша за 1 (не менша за 1)?

ЗМІСТ САМОСТІЙНОЇ РОБОТИ

Континуум-гіпотеза

Континуум-гіпотеза ще відома як перша проблема Гільберта, її формулювання наступне:

З точністю до еквівалентності, існують тільки два типи нескінченних числових множин - зліченна множина і континуум.

Інакше кажучи, потрібно встановити, чи існує множина проміжної потужності, тобто така множина 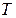, , 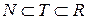яка не еквівалентна ні 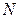, ні .

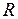Довести континуум-гіпотезу – значить, вивести її з системи аксіом. Спростувати її – значить, показати, що якщо її додати до цієї системи аксіом, то вийде суперечливий набір тверджень. У теорії множин є загальновизнана система аксіом Цермело–Френкеля.

Цією проблемою займалися дуже багато математиків. Г. Кантор неодноразово заявляв, що довів цю гіпотезу, але всякий раз знаходив у себе помилку.

Вирішення проблеми

Виявилось, що перша проблема Гільберта має абсолютно несподіване рішення.

У 1963 році американський математик Паул Коен довів, що континуум-гіпотезу не можна ні довести, ні спростувати.

Це означає, що якщо узяти стандартну систему аксіом Цермело–Френкеля (ZF) і додати до неї континуум-гіпотезу як ще одну аксіому, то вийде несуперечлива система тверджень. Але якщо до ZF додати заперечення континуум-гіпотези (тобто протилежне твердження), то знову вийде несуперечлива система тверджень.

Таким чином, ні континуум-гіпотезу, ні її заперечення не можна вивести із стандартної системи аксіом.

Що ж робити з цією гіпотезою? Зазвичай її просто приєднують до системи аксіом ZF. Але кожного разу, коли використовують при доведенні якогось твердження континуум-гіпотезу, обов’язково указують на це.

2. Підготуватися до обговорення статі «Редукция аксиом линейного пространства» [19]. дати відповіді на такі запитання:

· В якому сенсі в назві статті використане слово «редукция»;

· Які висновки можна зробити відносно системи аксіом векторного простору, відомої з курсу лінійної алгебри;

· Як з використанням запропонованої в статті системи аксіом довести такі теореми (задача 5 теми 1).

З. Теорема 26 з Додатку Г. Через точку, що належить даній прямій, можна провести перпендикуляр і тільки один. Яке з двох доведень підходить для розгляду цієї теореми після аксіом третьої групи системи Гільберта? В якому з доведень використовується 5 постулат?

Доведення 1. Від даної точки на кожній з півпрямих відкладемо рівні між собою відрізки 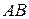і 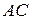. Від півпрямої 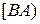відкладемо довільний гострий кут 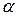. Від півпрямої 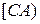відкладемо кут, рівний 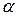. Отримаємо рівнобедрений трикутник. Проведемо медіану до сторони 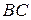, вона і буде перпендикуляром до даної прямої. Єдиність випливає із єдиності середини відрізка.

Доведення 2. Розглянемо будь-яку точку 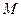, яка не належить заданій прямій. За теоремою 25 з неї можна опустити єдиний перпендикуляр на дану пряму, він утворює з даною прямою прямий кут. Всі прямі кути рівні між собою за теоремою 22. За аксіомо. 3.4 існує єдиний промінь з початком А, який утворює з променем даної прямої з початком А кут, рівний побудованому прямому куту.