Довести справедливість тверджень в геометрії Лобачевского

3.1. Будь-які дві паралельні прямі мають вісь симетрії.

3.2. Якщо пряма 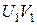паралельна прямій 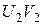, то пряма 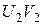паралельна прямій 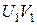(властивість симетричності відношення паралельності прямих на площині Лобачевского).

3.3. Якщо пряма 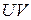лежить між паралельними прямими 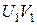і і 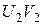не перетинає жодну з них, то вона їм паралельна.

3.4. Нехай пряма 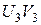симетрична прямій 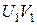відносно прямої 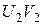, а прям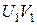і і 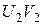паралельні між собою. Тоді пряма 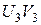паралельна як прямій 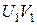так і прямий .

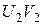3.5. Якщо пряма 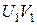паралельна прямій 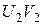і пряма 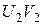паралельна прямій 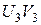, причому 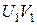і 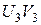- різні прямі, то пряма 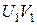паралельна прямій 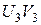(властивість транзитивності відношення паралельності прямих на площині Лобачевского).

3.6. У прямокутному трикутнику величина хоч би одного з його гострих кутів менше .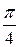

3.7. У прямокутному трикутнику катет, що лежить проти кута 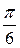, більше половини гіпотенузи.

3.8. Кут, під яким видно діаметр кола з будь-якої точки цього кола, не співпадаючого з кінцями діаметру, - гострий.

3.9. У рівносторонньому трикутнику пряма, на якій лежить його середня лінія, і пряма, що містить основу трикутника, розходяться.

3.10. Середня лінія трикутника менше половини його основи.

3.11. У чотирикутнику Саккері відрізок, що сполучає середини нижнього і верхнього підстав, менше бічної сторони.

3.12. У чотирикутнику Саккері кожна пара протилежних сторін належить прямим, що розходяться.

3.13. У довільному трикутнику пряма, що містить його середню лінію розходиться з прямою, що містить сторону, що не має загальних точок з цією середньою лінією;

3.14. У усіх трикутників, що мають цей кут a при вершині A, висоти ha обмежені нерівністю: 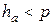, де 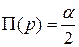– кут паралельності, що відповідає відрізку .

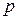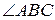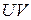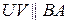3.15. Нехай – довільний кут, менший розгорнутого. Довести, що завжди існує така пряма , що і 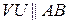(пряма, паралельна сторонам ).

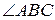ПІДСУМКОВИЙ ТЕСТ

1. Сума внутрішніх кутів трикутника на площині Лобачевского
a. дорівнює ,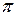
b. менша ,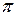
c. більша .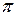

2. Вектор є основним поняттям в системі аксіом
a. Г. Вейля,
b. А. В. Погорєлова,
c. Д. Гільберта,
d. А. Д. Олександрова.

3. На площині Лобачевського між собою рівні всі
a. кола,
b. еквідистанти,
c. оріцикли.

4. Твердження «Через дану точку поза прямою можна провести не більше однієї прямої, що не перетинає дану» вірне в

a. геометрії Евкліда,

b. геометрії Лобачевского,

c. абсолютній геометрії.

5 . Подібних трикутників не існує в
a. геометрії Евкліда,
b. геометрії Лобачевского,
c. абсолютній геометрії.

6.У системі аксіом Вейля залежною є аксіома
a. асоціативності додавання векторів,
b. комутативності додавання векторів,
c. комутативності скалярного добутку векторів,
d. існування трьох лінійно незалежних векторів.

7. Відрізок є основним поняттям в системі аксіом
a. Г. Вейля,
b. А. В. Погорєлова,
c. Д. Гільберта,
d. А. Д. Олександрова.

8. В евклідовому просторі геометрія Лобачевського «в малому» реалізується на
a. сфері,
b. псевдосфері,
c. гелікоїді,
d. катеноїді.

9. Прямих, які не перетинаються, немає в

a. геометрії Евкліда,

b. геометрії Лобачевского,

c. абсолютній геометрії,

d. сферичній геометрії.

ЛІТЕРАТУРА

1. Александров А.Д. Геометрия / А.Д.Александров, С.К.Нецветаев. – М.: Наука, 1985. – 671 с.

2. Бакельман И.Я Высшая геометрия / И.Я.Бакельман. - М.: Просвещение, 1967. – 367 с.

3. Базылев В.Т. Сборник задач по геометрии / В.Т.Базылев, К.И.Дуничев, В.П.Иваницкая. - М.: Просвещение, 1980. – 238 с.

4. Беляев Е.А. Философские и методологические проблемы математики /Е.А.Беляев, В.Я.Перминов. – М.: Изд-во Моск. ун-та, 1981. – 217 с.

5. Болибрух А.А. Проблемы Гильберта (100 лет спустя) / А.А. Болибрух. – М.: МЦНМО, 1999. – 24 с.

6. Гильберт Д. Основания геометрии / Д. Гильберт. - М.: ГИТТЛ, 1948. – 152 с.

7. Егоров И.П. Геометрия / И.П.Егоров. – М.: Просвещение, 1979. – 256 с.

8. Ефимов Н.В. Высшая геометрия / Н.В.Ефимов. – М.: Наука, 1978. –576 с.

9. Кадомцев С.Б. Геометрия Лобачевского и физика / С.Б. Кадомцев. – М.: Изд-во ЛКИ, 2007. — 72 с.

10. Клини С.К. Введение в метаматематику / С.К.Клини. – М.: Мир, 2008. – 480 с. / http://www.bookshop.ua/

11. Кудрявцев Л.Д. Математический анализ. Т.1 / Л.Д.Кудрявцев. – М.: Высшая школа, 1970. – 592 с.

12. Курант Р. Что такое математика? Элементарный очерк идей и методов / Р. Курант, Г. Роббинс, – М.: МЦНМО, 2001. – 568с.

13. Лакатос И. Доказательства и опровержения. Как доказываются теоремы / И. Лакатос. – М.: Наука, 2010. – 154 с.

14. Нечаев В.И. Числовые системы / В.И.Нечаев. – М.: Просвещение, 1975. – 199 с.

15. Прасолов В.В. Геометрия Лобачевского / В.В.Прасолов. – М.: Наука, 2004, - 88 с.

16. Перминов В.Я. Философия и основания математики / В.Я. Перминов. – Прогресс-Традиция, 2001. – 320 с. /

http://www.knigka.info/2010/02/28/filosofija-i-osnovanija-matematiki.html

17. Франгулов С.А. Сборник задач по геометрии / С.А. Франгулов, П.И. Совертков, А.А. Фадеева, Т.Г. Ходот. – М.: Просвещение, 2002 – 263 с.

18. Шилов Г.Е. Математический анализ. Функции одного переменного / Г.Е.Шилов. – М.: Наука, 1969. – 528 с.

19.Lesniewicz R. Редукция аксиом линейного пространства / Вісник Харківського нац. ун-ту ім. В.Н.Каразіна. –серія «Математика, прикладна математика і механіка».- 2009.- №850. – С.78-82 / vestnik-math.univer.kharkov.ua/Vestnik-Khnu-850-2009-lesh.pdf