Довести, що п'ятий постулат Евкліда еквівалентний твердженню

2.1. Існує трикутник, сума внутрішніх кутів якого дорівнює двом прямим кутам.

2.2. Існує чотирикутник з чотирма прямими кутами.

2.3. Кут, під яким з точки кола видно її діаметр, дорівнює прямому куту.

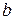2.4. Якщо прямі і , які перетинаються, не перпендикулярні, то перпендикуляр, проведений у будь-якій точці прямої , перетинає пряму .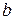

2.5.Перпендикуляри, проведені до середин сторін будь-якого трикутника, перетинаються в одній точці.

2.6. Біля довільного трикутника можна описати коло.

2.7. Відстань від змінної точки однієї з прямих до іншої прямої обмежена.

2.8. Перпендикуляр і похила до однієї прямої перетинаються.

2.9. Існує трикутник з сумою внутрішніх кутів, рівною двом прямим кутам.

2.10. Існує два подібні і нерівні трикутники.

2.11. Існує, принаймні, один квадрат.

2.12. Існує, принаймні, один опуклий чотирикутник з сумою внутрішніх кутів рівною чотирьом прямим кутам.

2.13. Сторона правильного шестикутника, вписаного в коло, дорівнює радіусу кола.

2.14. Три точки, рівновіддалені від цієї прямої і розташовані в одній півплощині відносно неї, належать одній прямій.

2.14. Теорема Піфагора.

2.15. Середня лінія трикутника паралельна основі і дорівнює його половині.