Приклади розв’язання задач
Задача 1.Довести справедливість твердження в геометрії Лобачевского: «Середня лінія трикутника менша половини його основи».
 Доведення. Розглянемо трикутник
Доведення. Розглянемо трикутник 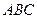 ,
, 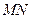 – середня лінія. Доведемо, що
– середня лінія. Доведемо, що 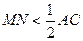 .
.
Через середини сторін 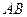 і
і 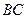 проведемо пряму і опустимо на неї перпендикуляри з вершин трикутника. Рівності
проведемо пряму і опустимо на неї перпендикуляри з вершин трикутника. Рівності 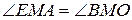 та
та 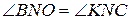 для пар вертикальних кутів і рівність за умовою відмічених пар відрізків дає можливість зробити висновок
для пар вертикальних кутів і рівність за умовою відмічених пар відрізків дає можливість зробити висновок 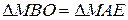 та
та 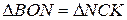 про рівність прямокутних трикутників (за гіпотенузою та гострим кутом). З цього випливає, що
про рівність прямокутних трикутників (за гіпотенузою та гострим кутом). З цього випливає, що 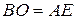 та
та 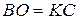 , тобто
, тобто 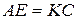 . Отриманий чотирикутник
. Отриманий чотирикутник 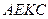 є чотирикутником Саккері. В цьому чотирикутнику
є чотирикутником Саккері. В цьому чотирикутнику 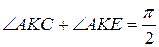 , тобто
, тобто 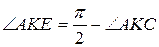 . В трикутнику
. В трикутнику 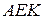 :
: 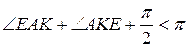 , тобто
, тобто 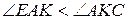 , звідки
, звідки 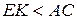 .
.
З того, що 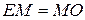 та
та 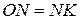 випливає, що
випливає, що 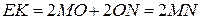 . Таким чином,
. Таким чином, 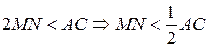 .
.
Задача 2.Довести справедливість твердження в геометрії Лобачевского: «Кут, під яким діаметр кола видно з будь-якої точки цього кола, відмінної від кінців діаметра, – гострий»

Доведення. Розглянемо коло з центром в точці 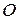 та діаметром
та діаметром 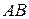 . Візьмемо на колі довільну точку
. Візьмемо на колі довільну точку 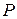 та розглянемо утворений трикутник
та розглянемо утворений трикутник 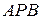 . З того, що
. З того, що 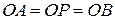 як радіуси випливає, що
як радіуси випливає, що 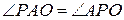 та
та 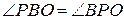 . Сума кутів трикутника в геометрії Лобачевского менша
. Сума кутів трикутника в геометрії Лобачевского менша 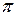 , тому
, тому

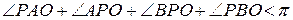 ,
,
Або 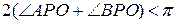 . Отже,
. Отже, 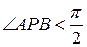 , тобто він гострий. Доведено.
, тобто він гострий. Доведено.
Задача 3. Довести справедливість твердження в геометрії Лобачевского: «В прямокутному трикутнику величина хоча б одного з його кутів менше 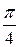 ».
».
Доведення. В прямокутному трикутнику один з кутів дорівнює 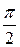 . Якщо припустити, що кожен з останніх двох кутів не менший за
. Якщо припустити, що кожен з останніх двох кутів не менший за 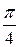 , то їх сума буде більшою за
, то їх сума буде більшою за 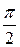 . Ми отримали суперечність, оскільки в геометрії Лобачевского сума внутрішніх кутів трикутника менша за
. Ми отримали суперечність, оскільки в геометрії Лобачевского сума внутрішніх кутів трикутника менша за 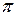 .
.
Задача 4. Довести твердження: «Якщо три кути одного трикутника дорівнюють відповідно трьом кутам другого трикутника, то такі трикутники рівні» (четверта ознака рівності трикутників.)

Доведення. Розглянемо трикутники 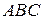 та
та 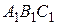 , в яких
, в яких 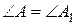 ,
, 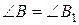 ,
, 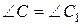 . Потрібно довести рівність відповідних сторін цих трикутників.
. Потрібно довести рівність відповідних сторін цих трикутників.
Припустимо, що 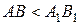 . Існує така точка
. Існує така точка 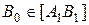 , що
, що 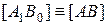 . Через точку
. Через точку 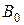 проведемо півпряму
проведемо півпряму 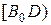 так, що
так, що 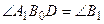 . За теоремою 46 пряма
. За теоремою 46 пряма 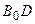 паралельна стороні
паралельна стороні 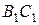 . За аксіомою Паша промінь
. За аксіомою Паша промінь 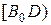 перетинає відрізок
перетинає відрізок 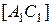 , позначимо точку перетину
, позначимо точку перетину 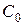 . Трикутники
. Трикутники 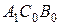 і
і 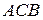 конгруентні (за теоремою 15). Ми довели, що трикутники
конгруентні (за теоремою 15). Ми довели, що трикутники 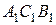 і
і 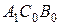 подібні та не конгруентні. Але твердження про існування подібних не конгруентних трикутників є еквівалентом п’ятого постулату Евкліда. Отже, отримали протиріччя, а значить
подібні та не конгруентні. Але твердження про існування подібних не конгруентних трикутників є еквівалентом п’ятого постулату Евкліда. Отже, отримали протиріччя, а значить 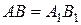 , звідки за теоремою 15 можемо зробити висновок про рівність даних трикутників.
, звідки за теоремою 15 можемо зробити висновок про рівність даних трикутників.
Задача 5. Довести, що існують такі трикутники, навколо яких не можна описати коло.
 Доведення. На площині Лобачевського проведемо прямі
Доведення. На площині Лобачевського проведемо прямі 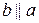 . Через точку
. Через точку 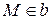 проведемо пряму
проведемо пряму 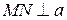 , яка з прямою
, яка з прямою  утворює кут
утворює кут 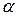 – кут паралельності . Візьмемо точку
– кут паралельності . Візьмемо точку 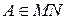 , побудуємо точку
, побудуємо точку 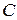 , яка симетрична точці
, яка симетрична точці  відносно прямої
відносно прямої 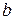 та точку
та точку 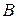 , яка симетрична точці
, яка симетрична точці  відносно прямої
відносно прямої  . Точки
. Точки 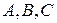 не належать одній прямій, оскільки в противному випадку
не належать одній прямій, оскільки в противному випадку 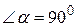 , що неможливо для кута паралельності. Розглянемо трикутник
, що неможливо для кута паралельності. Розглянемо трикутник 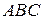 . В ньому пряма
. В ньому пряма  є серединним перпендикуляром до сторони
є серединним перпендикуляром до сторони 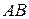 , пряма
, пряма 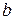 є серединним перпендикуляром до сторони
є серединним перпендикуляром до сторони 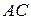 та
та 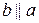 за умовою, тому навколо цього трикутника не можна описати коло.
за умовою, тому навколо цього трикутника не можна описати коло.
Задача 5.Довести, що ортогональна проекція однієї зі сторін гострого кута на іншу сторону є півінтервалом.

Доведення. Розглянемо гострий кут 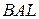 . Відомо, що яким би не був гострий кут, завжди існує єдина пряма, перпендикулярна до сторони
. Відомо, що яким би не був гострий кут, завжди існує єдина пряма, перпендикулярна до сторони 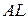 цього кута і паралельна стороні
цього кута і паралельна стороні 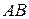 . Отже, точка С не є ортогональною проекцією жодної з точок прямої
. Отже, точка С не є ортогональною проекцією жодної з точок прямої 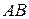 на сторону
на сторону 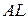 кута, а кожна з точок півінтервала
кута, а кожна з точок півінтервала 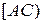 буде ортогональною проекцією деякої точки сторони
буде ортогональною проекцією деякої точки сторони 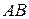 .
.
Дата добавления: 2016-12-08; просмотров: 1202;
