Приклади розв’язання задач
Задача 1. Довести що коли прямі 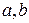 і
і 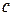 лежать в одній площині і пряма
лежать в одній площині і пряма 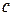 , яка перетинає прямі
, яка перетинає прямі 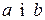 , утворює з ними рівні внутрішні навхрест лежачі кути, то прямі паралельні.
, утворює з ними рівні внутрішні навхрест лежачі кути, то прямі паралельні.

Доведення. Нехай пряма 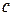 перетинає пряму
перетинає пряму 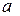 в точці
в точці  , а пряму
, а пряму 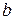 – в точці
– в точці 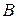 . Скористаємося методом від супротивного. Припустимо, що існує така точка
. Скористаємося методом від супротивного. Припустимо, що існує така точка 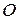 , що прямі
, що прямі 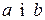 перетинаються в ній. В утвореному трикутнику
перетинаються в ній. В утвореному трикутнику  кут
кут 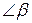 – внутрішній кут при вершині
– внутрішній кут при вершині 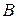 ,
,  кут
кут 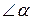 – зовнішній кут при вершині
– зовнішній кут при вершині  і
і 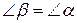 (за умовою). Отримали протиріччя з теоремою 30, отже наше припущення невірне, тобто прямі
(за умовою). Отримали протиріччя з теоремою 30, отже наше припущення невірне, тобто прямі 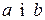 не перетинаються.
не перетинаються.
Задача 2.Довести, що для чотирикутника Саккері виконуються наступні твердження:
1. серединний перпендикуляр до нижньої основи перетинає верхню основу;
2. серединний перпендикуляр до нижньої основи є серединним перпендикуляром до верхньої основи;
3. Кути при верхній основі рівні.

Доведення.
1. У чотирикутнику Саккері розглянемо трикутник 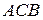 і серединний перпендикуляр
і серединний перпендикуляр 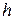 до нижньої основи. Пряма
до нижньої основи. Пряма 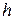 за умовою перетинає відрізок
за умовою перетинає відрізок 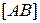 , пряма
, пряма 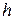 і відрізок
і відрізок 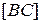 не перетинаються за теоремою 45. Отже, пряма
не перетинаються за теоремою 45. Отже, пряма 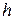 і відрізок
і відрізок 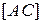 перетинаються (за аксіомою Паша). Далі розглянемо трикутник
перетинаються (за аксіомою Паша). Далі розглянемо трикутник 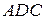 . З того, що
. З того, що 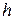 і
і 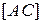 перетинаються, а
перетинаються, а 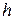 і
і 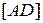 не перетинаються, випливає, що
не перетинаються, випливає, що 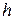 і
і 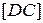 перетинаються.
перетинаються. 
2. Розглянемо трикутники 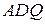 і
і 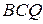 . За умовою
. За умовою 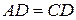 ,
, 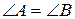 ,
, 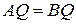 , а значить
, а значить 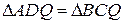 (за теоремою 14). З рівності трикутників випливає, що
(за теоремою 14). З рівності трикутників випливає, що 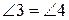 ,
, 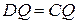 . Оскільки
. Оскільки 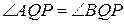 , то
, то 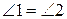 . За теоремою 14 виконується також рівність трикутників
. За теоремою 14 виконується також рівність трикутників 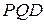 і
і 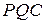 , а значить
, а значить 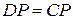 ,
, 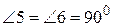 (як суміжні). Отже,
(як суміжні). Отже, 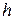 – серединний перпендикуляр до
– серединний перпендикуляр до 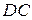 .
.
3. З рівності 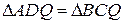 випливає, що
випливає, що 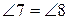 , а з
, а з 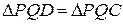 випливає, що
випливає, що 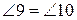 . Тому
. Тому 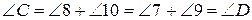 .
.
Задача 3.Довести, що верхня основа чотирикутника Саккері не менша за нижню.

Доведення. В чотирикутнику 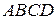 позначимо кути:
позначимо кути: 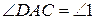 ,
, 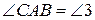 ,
, 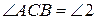 . В абсолютній геометрії має місце теорема: сума кутів трикутника не більша ніж
. В абсолютній геометрії має місце теорема: сума кутів трикутника не більша ніж 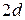 . Тому можна записати наступні співвідношення
. Тому можна записати наступні співвідношення 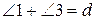 ,
, 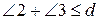 ,з яких слідує
,з яких слідує 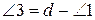 і
і 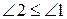 . З останньої нерівності посилаючись на теорему 32 робимо висновок, що
. З останньої нерівності посилаючись на теорему 32 робимо висновок, що 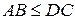 .
.
Задача 4.Довести, що середня лінія трикутника не більша за половину основи.

Доведення. Нехай в трикутнику 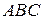 побудована середня лінія
побудована середня лінія 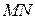 . На пряму
. На пряму 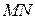 опустимо перпендикуляри з вершин трикутника Трикутники
опустимо перпендикуляри з вершин трикутника Трикутники 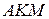 і
і 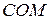 рівні, тому
рівні, тому 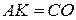 . Також виконується рівність
. Також виконується рівність 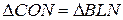 , а значить
, а значить 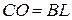 , отже
, отже 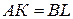 . Отриманий чотирикутник
. Отриманий чотирикутник 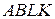 є чотирикутником Саккері, а тому
є чотирикутником Саккері, а тому 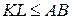 за попередньою задачею. З рівності вказаних пар трикутників випливають рівності
за попередньою задачею. З рівності вказаних пар трикутників випливають рівності 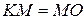 ,
, 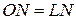 відповідних сторін цих трикутників.
відповідних сторін цих трикутників.
Таким чином, 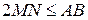 , або
, або 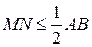 , що і треба було довести.
, що і треба було довести.
Задача 5. Довести, якщо два серединних перпендикуляра до сторін трикутника перетинаються в точці 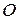 , то і третій серединний перпендикуляр проходить через цю точку.
, то і третій серединний перпендикуляр проходить через цю точку.
 Доведення.Розглянемо трикутник
Доведення.Розглянемо трикутник 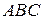 , в якому
, в якому  – серединний перпендикуляр до сторони
– серединний перпендикуляр до сторони 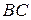 ,
, 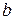 – серединний перпендикуляр до сторони
– серединний перпендикуляр до сторони 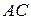 та прямі
та прямі  і
і 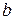 перетинаються в точці
перетинаються в точці 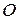 Проведемо серединний перпендикуляр
Проведемо серединний перпендикуляр 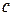 до сторони
до сторони 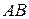 . Розглянемо трикутники
. Розглянемо трикутники 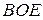 та
та 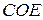 , вони рівні за першою ознакою рівності трикутників. Аналогічно
, вони рівні за першою ознакою рівності трикутників. Аналогічно 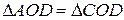 . З цих рівностей випливає, що
. З цих рівностей випливає, що 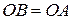 , а значить трикутник
, а значить трикутник  – рівнобедрений. Нехай
– рівнобедрений. Нехай 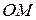 – медіана цього трикутника, тоді за теоремою 17 bis
– медіана цього трикутника, тоді за теоремою 17 bis 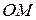 та
та 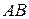 перпендикулярні, тобто
перпендикулярні, тобто 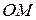 співпадає з серединним перпендикуляром
співпадає з серединним перпендикуляром 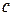 .
.
Дата добавления: 2016-12-08; просмотров: 996;
