Аксіоматична теорія псевдоевклідової геометрії. Класифікація прямих і площин псевдоевклідового простору. Основні координатні формули.

Псевдоевклідів тривимірний простір індексу 1, який будемо позначати символом 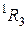, можна визначити як множину елементів двох родів, які називаються точками і векторами, з уведеними операціями додавання векторів, множення вектора на дійсне число, відкладання вектора від точки і скалярного добутку векторів, що задовольняють аксіомам I-IV груп, 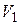, , 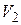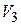аксіоматика Вейля (Додаток А) і аксіомі .

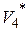Аксіома. 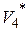. Існують три попарно ортогональних вектори 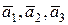такі, що .

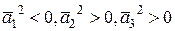Домовимось, як і в евклідовому просторі, називати два вектора ортогональними, якщо їх скалярний добуток дорівнює нулю.

Означення. Вектори простору 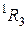, скалярні квадрати яких додатні, називаються евклідовими векторами. Вектори з від’ємними скалярними квадратами називаються псевдоевклідовими векторами. Ненульові вектори, скалярні квадрати яких дорівнюють 0, називаються ізотропними векторами. Згідно з визначенням ізотропних векторів два колінеарних ізотропних вектора ортогональні.

Довжину вектора будемо визначати, як і в евклідовому просторі, формулою 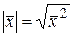. Так як в просторі 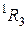скалярні квадрати векторів можуть бути додатними, від’ємними та рівними нулю, то з формули довжини вектора випливає, що ненульові вектори в цьому просторі можуть мати дійсну довжину (якщо 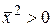), уявну довжину (якщо 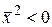) та нульову довжину (якщо ).

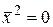У псевдоевклідовому просторі при нормуванні евклідового вектора будемо використовувати формулу 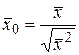, а при нормуванні псевдоевклідового вектора – формулу .

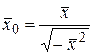Нормовані евклідові вектори прийнято називати одиничними, а нормовані псевдоевклідові вектори – уявно одиничними. Всі ізотропні вектори будемо вважати нормованими.

Із аксіоми 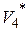випливає, що в просторі 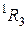завжди існує ортонормований базис, який складається з одного уявно одиничного і двох одиничних векторів. Умовимося уявно одиничний вектор вибирати першим вектором базису. Неважко показати, що всі ортогональні базиси простору складаються з одного псевдоевклідового і двох евклідових векторів, тобто має місце закон інерції ортогональних базисів.

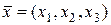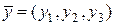Координати векторів в ортонормованому базисі будемо так само, як і в евклідовому просторі, називати декартовими. Скалярний добуток векторів і , заданих декартовими координатами, має вигляд: 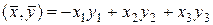, а скалярний квадрат вектора :

.

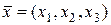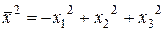Перейдемо до питання про класифікацію площин простору 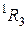. Її зручно проводити з використанням поняття ізотропного конуса. Відкладемо всі вектори простору 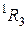від початку координат. Тоді кінці ізотропних векторів будуть лежати на поверхні

,

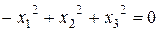яку називають ізотропним конусом. Кінці евклідових радіус-векторів лежать у зовнішній області ізотропного конуса, а кінці псевдоевклідових радіус-векторів – в його внутрішній області.

Прямі псевдоевклідового простору 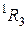діляться на три типи:

– евклідові, якщо довжина направляючого вектора дійсна;

– псевдоевклідові, якщо довжина напрямного вектора уявна;

– ізотропні, якщо довжина напрямного вектора дорівнює 0.

Для класифікації двовимірних площин дослідимо властивості ортогональних векторів. У просторі 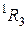ортогональними можуть бути пара евклідових векторів, евклідів і псевдоевклідів вектори, евклідів і ізотропний вектори. Неважко навести приклади таких пар.

Розглянемо в просторі 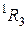двовимірні площини (далі площині), в яких всі вектори евклідові і площини, в яких є вектори всіх трьох типів. Називатимемо їх відповідно евклідовими і псевдоевклідовими площинами. Евклідові та псевдоевклідові площині називаються неізотропними. У просторі 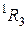можливі також площини, в яких є тільки евклідові та ізотропні вектори. Вони називаються ізотропними площинами. Розглянемо два неколінеарних вектори 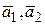в просторі 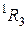. Вони утворюють направляючий підпростір деякої двовимірної площини. Щоб визначити тип цієї площини, потрібно розглядати всілякі лінійні комбінації векторів. Але якщо на базі цих векторів побудувати ортогональну систему векторів, то в разі евклідової площини, ця система обов'язково складається з евклідових векторів, у разі псевдоевклідової площини – з псевдоевклідового і евклідового векторів, у випадку ізотропної площини – з ізотропного і евклідового векторів. Тобто тип площини легко розпізнавати по набору з двох ортогональних направляючих векторів.

Зауважимо, що площина, яка містить вершину ізотропного конуса і не має з ізотропним конусом інших спільних точок, є евклідовою. Якщо ж вона перетинає ізотропний конус по двом твірним, то така площина псевдоевклідова. Площина, яка дотикається ізотропного конуса по твірній, є ізотропною.