Елементи сферичної геометрії. Точки і прямі в сферичній геометрії. Відстань між точками і кут між прямими.

Нехай в евклідовому просторі задано сферу радіусу 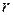. В геометрії на сфері, як і в геометрії на евклідовій площині, основними об’єктами є точки і прямі. «Точкою» називається будь-яка точка сфери, «прямою» – будь-яке велике коло сфери.

Означення. Нехай 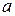– деяка пряма в сферичній геометрії. Кінці 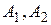діаметра сфери, перпендикулярного евклідовій площині, яка містить 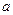, називаються полюсами цієї прямої. Кожна точка прямої 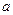називається полярно спряженою з кожним із її полюсів.

Через будь-які дві не діаметрально протилежні точки проходить єдина пряма сферичної геометрії.

Означення. Відстанню між точками називається довжина меншої з двох дуг великого кола, що проходить через ці точки.

З означення випливає обмеженість сферичної площини – відстань між будь-якими двома точками не перевищує числа .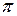

Крім основних об’єктів в сферичній геометрії можна розглядати і інші фігури. Наприклад, Коло на сфері, яке не є великим, задовольняє означення кола з евклідової геометрії.

Означення.Кутом 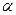між двома прямими в сферичній геометрії називається двогранний кут, який утворюють евклідові площини, що містять ці прямі.

Засобами евклідової геометрії отримується формула

,

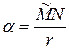де точки 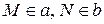– полярно спряжені з точкою перетину прямих.