Сфери псевдоевклідового простору. Сферична тригонометрія.

Визначення сфери в псевдоевклідовому просторі залишимо таким самим, як і в евклідовому просторі, тобто як множину точок, що знаходяться на однаковій відстані від фіксованої точки. У зв'язку з тим, що відстань в просторі 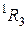обчислюється за іншою формулою, то рівняння сфери псевдоевклидового простору з центром у початку координат і радіусом 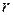буде мати вигляд 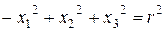. Будемо розглядати сфери дійсного та уявного радіуса.

Сфера дійсного радіусу псевдоевклідового простору зображується в евклідовому просторі однопорожнинним гіперболоїдом

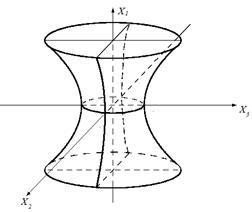
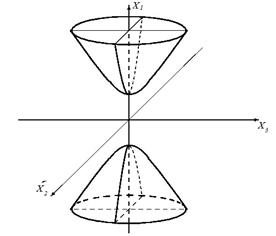
Сфера уявного радіуса псевдоевклідового простору зображується в евклідовому просторі двопорожнинним гіперболоїдом.

Формули сферичної геометрії в евклідовому і псевдоевклідовому просторах однакові, але зміст їх різний. Крім того, сфера уявного радіусу несе на собі геометрію Лобачевського.

5. Інтерпретація планіметрії Лобачевського на сфері уявного радіусу псевдоевклідового простору. Евклідова геометрія як граничний випадок геометрії Лобачевського

Встановимо наступний словник. Під «точкою» будемо розуміти дві діаметрально протилежні точки сфери. Або можна поступити інакше. Другу порожнину сфери уявного радіусу не розглядати та інтерпретувати геометрію Лобачевського на півсфері. «Пряма» – це лінія перетину півсфери з площиною, що проходить через початок координат. Оскільки вся півсфера лежить у внутрішній області ізотропного конуса, то для кожної точки півсфери її радіус-вектор є псевдоевклідовим, тобто .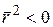

Покажемо, що при цих домовленостях про зміст точок та прямих півсфера уявного радіусу псевдоевклідового простору несе на собі геометрію площини Лобачевського. Для того, щоб упевнитися в цьому, треба перевірити виконання всіх аксіом планіметрії Лобачевського. Обмежимось перевіркою аксіоми паралельності. Передусім треба встановити зміст термінів «прямі, що перетинаються», «прямі, що розходяться» та «паралельні прямі» для даної інтерпретації.

Оскільки прямі, які перетинаються, повинні мати спільну точку, то площини зв’язки з центром в точці О, які їх визначають, повинні перетинатися по прямій, яка проектує цю точку, але така пряма є псевдоевклідовою, тому що лежить всередині ізотропного конусу.

У відповідності з визначенням паралельних прямих по Лобачевському проектуючі їх площини зв’язки повинні перетинатися по ізотропній прямій, тобто по твірній ізотропного конуса.

Прямі, що розходяться, належать двома площинам, які перетинаються по евклідовій прямій.

Перевірка аксіоми паралельності Лобачевського дає позитивну відповідь, аксіома виконується на сфері уявного радіусу псевдоевклідового простору.

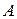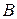Розглянемо деякі формули геометрії Лобачевського. Оскільки вона реалізується на сфері, то можна використовувати формули сферичної геометрії. В сферичній геометрії відстань між двома точками і знаходиться за формулою

,

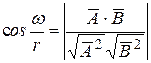де 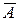і 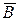– радіус-вектори цих точок. Застосуємо її до сфери уявного радіусу 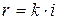, тоді 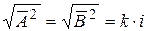, 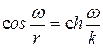і формула має вигляд

.

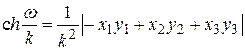Оскільки площа трикутника на сфері обчислюється за формулою 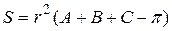, то при 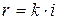ця формула буде мати вигляд

.

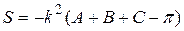Звідси отримуємо важливий і вже відомий нам висновок для суми внутрішніх кутів трикутника:

.

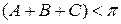Різницю 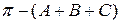називають дефектом трикутника та позначають 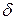. Тоді 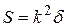, тобто площа трикутника пропорційна його дефекту.

Нагадаємо, що перша теорема косинусів для сфери має вигляд 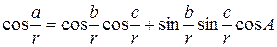. Якщ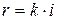о , то 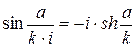. Тоді теорема косинусів для сфери уявного радіусу має вигляд

.

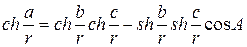З другої теореми косинусів на сфері отримаємо другу терему косинусів на площині Лобачевського:

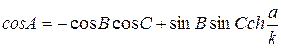
Теорема синусів на площині Лобачевського запишеться у вигляді

.

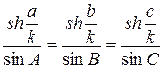Виведемо основну формулу геометрії Лобачевського. Розглянемо трикутник.

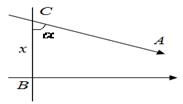
Застосуємо до нього другу терему косинусів, враховуючи, що 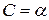, , 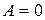, 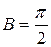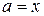. Отримаємо 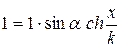, звідки 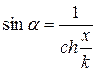та 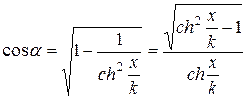. Після застосування формули 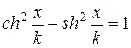ця рівність набуде вигляду 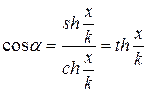. Далі запишемо

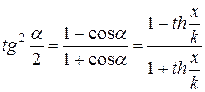. Відомі також формули 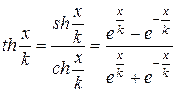.Тоді 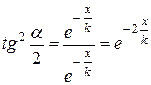, звідки 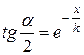–основна формула геометрії Лобачевського.