Г) Сутність проблеми 5 постулату Евкліда. Еквівалентність аксіоми паралельності та п’ятого постулату Евкліда. Інші еквіваленти п’ятого постулату.

5 п. Якщо при перетині двох прямих третьою сума двох внутрішніх односторонніх кутів менша за 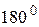, то ці прямі перетинаються з тієї сторони, з якої ця сума менша за .

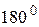5 п. 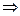V.Якщо має місце 5 постулат Евкліда, то через кожну точку, яка не належить довільно заданій прямій, проходить не більше однієї прямої, що не перетинає дану пряму.

Доведення. Нехай 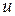- дана пряма, 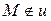і ,

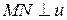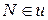
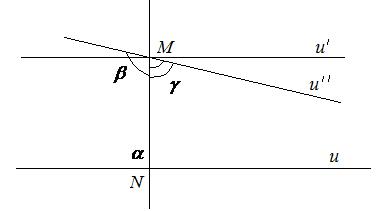
1).За теоремою 44 існує пряма 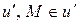, яка паралельна прямій .

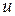2) Доведемо, що будь-яка інша пряма 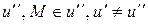не може бути паралельною прямій .

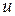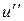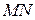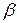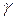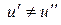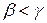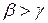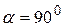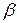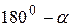3) Нехай півпрямі прямої утворюють з перпендикуляром суміжні кути та . Оскільки , то має місце одна з нерівностей або . Пари кутів і , і 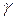є внутрішніми односторонніми при перетині прямих 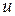та 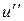прямою 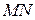. Ми довели, що одна із сум 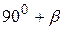і 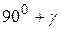менша за .

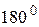4) За умовою має місце 5 постулат Евкліда. Отже, прямі 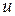та 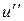перетинаються в тій півплощині відносно прямої 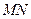, яка містить внутрішні односторонні кути з меншою за 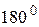сумою.

Ми довели, що пряма 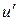єдина, тобто має місце аксіома паралельності V.

V 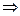5 п.Якщо через кожну точку, що не належить довільно заданій прямій, проходить рівно одна пряма, паралельна даній, то має місце 5 постулат Евкліда.

Доведення. Нехай 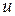- дана пряма, .

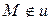1) За умовою через точку 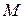проходить лише одна пряма, паралельна 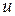, позначимо її 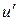. Отже, будь-яка пряма 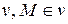перетинає пряму .

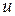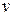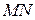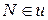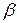2) Нехай півпрямі прямої утворюють з довільною півпрямою , кути та 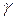, причому нехай для визначеності 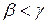. Тоді одна з півпрямих прямої 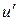є внутрішньою півпрямою кута .

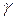3) Позначимо символом 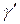кут між цією півпрямою та півпрямою 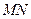, а рівний йому навхрест лежачий кут при перетині прямих 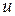та 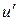прямою 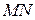– символом 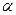. Тоді .

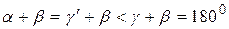4) Нехай пряма 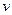перетинає пряму 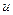в півплощині, яка містить кут 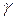і 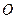– точка перетину. Тоді для трикутника 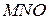кут 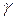є внутрішнім, а кут 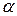– несуміжним із ним зовнішнім кутом. Оскільки 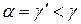, то маємо протиріччя із теоремою про зовнішній кут трикутника.

Отже, пряма 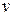перетинає пряму 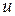в півплощині, яка містить кути 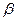та 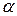, що і доводить справедливість 5 постулату Евкліда.

Наведемо список еквівалентів 5 постулату Евкліда в тій послідовності, в якій їх зручно доводити, посилаючись на попередні.

П.1. Перпендикуляр і похила, проведені до однієї прямої в одній площині, обов’язково перетинаються (твердження Лежандра).

П.2. Два серединних перпендикуляри до сторін трикутника завжди перетинаються.

П.3. Навколо кожного трикутника можна описати коло (твердження Ф. Бойяї).

П.4. Сума внутрішніх кутів будь-якого трикутника дорівнює .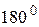

П.5. Сума внутрішніх кутів будь-якого трикутника одна і та сама.

П.6. Існують два подібних і не конгруентних трикутники.

П.7. Існують принаймні один прямокутник і один квадрат.

П.8. Існує принаймні один опуклий чотирикутник із рівною 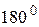сумою внутрішніх кутів.

П.9. Сторона правильного вписаного в коло шестикутника дорівнює радіусу цього кола.

П.10. Три різні точки, рівновіддалені від даної прямої і розташовані в одній півплощині відносно цієї прямої, належать одній прямій (колінеарні).