Побудова теорії дійсного числа за Дедекіндом.

Неперервність в сенсі Дедекінда пов’язана з поняттям перерізу множини.

Всі аксіоми перших трьох груп системи із Додатку Ґ залишимо без зміни.

Означення.Перерізом впорядкованої множини М є представлення цієї множини у вигляді 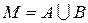, де підмножини 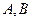називають класами і вони мають властивості:

1) кожний клас непорожній;

2) кожний елемент множини М належить тільки одному з класів;

3) якщо 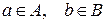, то .

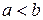Переріз позначають символом 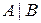, клас 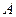називається лівим, клас 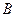– правим.

Доповнимо систему з перших трьох груп такою аксіомою.

Аксіома (Дедекінда).Кожне число з множини 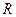визначає переріз множини 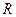і для всякого перерізу цієї множини існує число 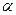, яке і здійснює цей переріз. Це число є або найбільшим у лівому класі (і тоді у правому класі немає найменшого), або найменшим у правому класі (і тоді у лівому класі немає найбільшого).

Отримаємо ще одну систему аксіом множини дійсних чисел, наслідками якої є всі відомі властивості дійсних чисел. В цій аксіоматичній теорії можна отримати як теореми твердження про вкладенні відрізки, аксіому Архімеда.

Ми ж зупинимось на одному з конструктивних підходів до теорії дійсного числа – побудові дійсних чисел за допомогою Дедекіндових перерізів. При цьому підході властивість неперервності (у наведеному вище формулюванні) доводиться в якості теореми.

Доведенняпобудуємо, спираючись на систему аксіом з Додатку Ґ.З вимоги 3) означення перерізу випливає, що множини 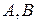не перетинаються. Якщо вибрати будь-яке дійсне число 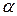і до класу 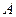віднести всі числа, менші за 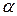, до класу 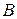– всі числа, більші за 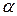, а саме число 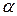– до будь-якого з цих двох класів. Тоді можемо говорити, що число 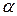здійснює переріз і позначати 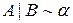, тобто перше твердження доведене.

Нехай тепер 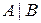– деякий переріз множини дійсних чисел. За другою вимогою означення, якщ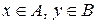о , то 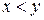. Таким чином, 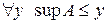, звідки 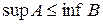. Рівність неможлива, тому що в противному випадку 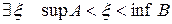, причому 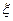не належить жодному з класів, що неможливо. Отже, число 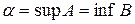здійснює заданий переріз 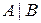[14]. Можливі два випадки: 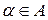або .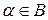

Покажемо, що неможливий переріз третього типу. Нехай 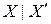– переріз в 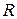. Позначимо символом А множину раціональних чисел, що належать Х, 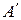– множину раціональних чисел, що належать 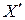. Нехай .

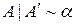1) якщо 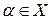, те воно найбільше в цьому класі. Припустимо противне. Нехай існує 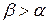і . І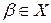снує раціональне число 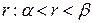. Оскільки 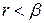, то 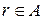. Оскільки 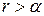, то 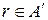. Отримали протиріччя.

2) якщо 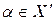, то воно найменше в цьому класі. Припустимо противне. Нехай існує 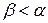і . І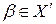снує раціональне число 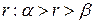. Оскільки 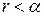, то 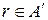. Оскільки 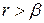, то 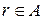. Отримали протиріччя.

Таким чином, в 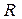немає "щілин", як у множині раціональних чисел. Ця властивість і називається неперервністю множини дійсних чисел.