Тема 3. Огляд і порівняння різних аксіоматичних теорій дійсних чисел.

Мета.Розглянути різні підходи до означення дійсного числа, ознайомитись із властивістю неперервності множини дійсних чисел.

План.

1. Огляд побудов теорії дійсного числа. Перші наслідки з аксіом.

2. Побудова теорії дійсного числа за Дедекіндом.

3. Роль аксіоми неперервності в побудові математичного аналізу.

Ключові поняття:дійсне число, послідовність, система вкладених відрізків, переріз у множині дійсних чисел.

Огляд побудов теорії дійсного числа.

Теорію дійсних чисел теж можна будувати аксіоматично.

Означення. Сукупність елементів називається множиною дійсних чисел, якщо на ній уведені операції додавання і множення елементів, відношення порядку, які задовольняють системі аксіом (наприклад, із Додатку Ґ).

Історично відомі кілька аксіоматичних означень множини дійсних чисел. Принципово системи аксіом в цих означеннях відрізняються лише тим, як в них постулюється властивість неперервності множини дійсних чисел. У аксіоматичному підході неперервність дійсних чисел виділена явно в окрему аксіому.

Неперервність множини дійсних чисел в сенсі Кантора вводиться шляхом означення поняття вкладених відрізків і формулювання відповідної аксіоми 5.1 (Додаток Ґ).

Іншим варіантом формулювання неперервності множини дійсних чисел є аксіома про верхню грань:будь-яка обмежена зверху підмножина А множини має точну верхню грань [18].

Відмітимо, що прийняття одного з можливих підходів для формулювання аксіоми неперервності множини дійсних чисел вимагає, згідно із сутністю аксіоматичного методу, доведення тверджень, які є іншими формулюваннями цієї аксіоми.

З системи аксіом множини дійсних чисел із Додатку Ґ виведемо, наприклад, такі твердження.

Теорема. .

Дійсно, доведенням теореми є система перетворень , якіможна виконати на основі аксіом 1.3, 1.4, 2.5, 1.4, 1.3.

Теорема. .

За аксіомою 1.4 . За попередньою теоремою і аксіомою 1.4 отримаємо 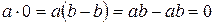, що і треба довести.

Теорема.Обернений до елемента дорівнює .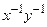

Знайдемо добуток 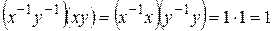, отже, , що і треба було довести.

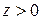Теорема.Якщо , то для будь-якого виконується нерівність .

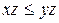Доведемо, що . Дійсно, за першою з доведених теорем 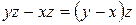. Враховуючи умову і аксіому 3.5, робимо висновок . Залишилось додати до обох частин цієї нерівності число 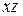, протилежне до числа 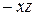, і застосувати аксіому 1.4.

Теорема.Для будь-яких існує ціле 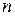таке, що .

Дійсно, оскільки 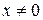, то існує частка 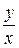, і тоді за аксіомою Архімеда існує таке ціле 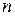, що 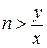, звідки за попередньою теоремою.