Ціле число - це клас попарно рівних між собою впорядкованих пар.

Теорема.Додавання цілих чисел комутативне і асоціативне.

Теорема.Множення цілих чисел комутативне, асоціативне і дистрибутивне по відношенню до додавання.

Доведення легко проводиться на мові пар.

Означення.Різницею цілого числа 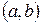і цілого числа називається таке ціле число , що .

Теорема.Різниця цілих чисел завжди існує і єдина.

Доведеннявипливає з формули

,

яку неважко отримати, використовуючи означення різниці.

Розглянемо цілі числа, друга компонента яких дорівнює 0, тобто множину 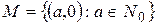. Легко отримати рівності:

,

,

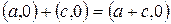, якщо .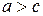

Тобто, якщо ввести взаємно однозначну відповідність 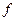за правилом , то для неї виконуються вимоги ізоморфізму. З’ясувалося, що множина М ізоморфна множині , або, інакше, що множина є підмножиною множини 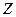. А це, в свою чергу, означає, що 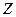є розширенням множини і важливо відмітити, що в цьому розширенні операція віднімання чисел завжди виконується.

В силу введеної відповідності 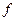рівність можна переписати у вигляді

,

який будемо називати другою формою запису цілого числа.

Означення.Будь-яке ціле число, менше за число 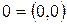, називається від’ємним.

За аксіомою 1.2) отримаємо

,

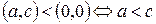тобто від’ємним є ціле число, в якому перша компонента менша за другу.

Віднявши від обох компонент від’ємного числа його першу компоненту, отримаємо 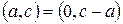, 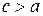. Якщо ввести позначення 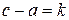, то від’ємне ціле число набуде вигляду . Це дає можливість продовжити введену відповідність 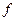на множину від’ємних чисел. Дійсно, якщо замість писати різницю (друга форма запису цілого числа), то очевидно відповідність буде взаємно однозначною і на множині від’ємних чисел. Фактично, ми ввели поняття знаку цілого числа.

Теорема. Добуток двох цілих чисел одного знаку є додатним цілим числом (натуральним числом). Добуток двох цілих чисел різних знаків є від’ємним цілим числом.

У сформульованій властивості цілих чисел легко переконатись, якщо задавати цілі числа парами.

Далі можна довести властивості нерівностей, ввести дії над нерівностями, означити операцію ділення цілих чисел і показати, що ця операція не завжди виконується в множині 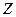. Отже, знову виникає ситуація необхідності розширення множини.