Огляд системи аксіом Вейля. Доведення несуперечливості системи аксіом Вейля евклідової геометрії.

В 1918 році німецьким математиком Г.Вейлем була запропонована точково-векторна аксіоматика евклідової геометрії (Додаток А).

Основними об’єктами системи аксіом Вейля є «точка» та «вектор». Основними відношеннями є «додавання векторів», «множення вектора на число», «скалярний добуток векторів», «відкладання вектора від точки». Аксіоматика Вейля складається з п’яти груп аксіом. Аксіоми перших трьох груп складають аксіоматику векторного простору, перших чотирьох груп – аксіоматику векторного евклідового простору, всю систему аксіом називають ще системою аксіом евклідового точково-векторного простору.

Несуперечливість системи аксіом Вейля доводиться шляхом побудови арифметичної моделі. В цій моделі «точкою» і «вектором» називають будь-яку впорядковану трійку дійсних чисел. При цьому для позначення точок будемо використовувати круглі дужки. Наприклад, точкою 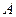є трійка . Для позначення векторів використовують кутові дужки. Наприклад, вектором є трійка .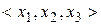

Для основного відношення першої групи введемо таке означення: сумою векторів 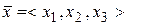та будемо називати вектор . Можна переконатися, що таке означення для суми векторів забезпечує виконання аксіом 1.1-1.4.

Множення дійсного числа 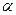на вектор (або вектора 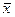на число 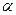) визначається наступним чином: 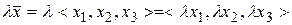. Так визначена операція задовольняє всім аксіомам другої групи

В третій групі основного відношення немає. Розглянемо набір векторів , , 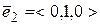, 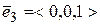він утворює базис тривимірного простору. Крім цього, для будь-якого вектора 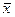цього простору маємо , тобто вектори , , , лінійно залежні. Аксіома розмірності виконується.

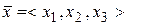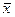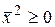Скалярним добутком векторів та називається число . Перші три аксіоми четвертої групи перевіряються безпосередньо. Скалярний квадрат вектора має вигляд , звідки випливає, що і що .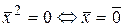

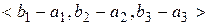Відношення п’ятої групи визначається так: будь-якій парі точок та відповідає вектор , який будемо позначати символом 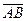. В аксіомі 5.1 задано ненульовий вектор та точка . Легко переконатись, що точка 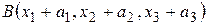задовольняє цю аксіому. Справедливість аксіоми 5.2 перевіряється безпосередньо.

Отже, можемо зробити висновок: система аксіом Вейля несуперечлива, якщо несуперечлива арифметика дійсних чисел.