Аксіоми ймовірності та її властивості
Означення 1. Ймовірністю називається числова функція P(A), визначена на множині всіх подій, пов’язаних з даним експериментом, яка задовольняє таким аксіомам:
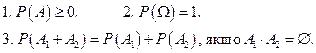
|
Аксіома 3 допускає узагальнення на випадок суми скінченної (або зліченної) кількості попарно несумісних подій:
3¢. P(A1+ A2+ A3+...+An) = P(A1)+P(A2)+P(A3)+...+P(An). (2)
Із аксіом 1,2,3 випливають такі властивості ймовірності:
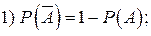
Дійсно: А + 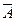 = Ω , А
= Ω , А 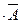 =Ø
=Ø 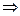 P(A+
P(A+ 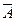 ) =P(A)+P(
) =P(A)+P( 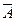 )=1
)=1 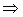
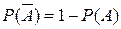 . Зокрема, P(Ø)=P(
. Зокрема, P(Ø)=P( 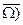 =1–P(Ω)=0.
=1–P(Ω)=0.
Звернемо увагу на те, що з рівності P(A)=0, взагалі кажучи, не випливає, що А є неможливою подією (випливає лише те, що частота цієї події при зростанні кількісті випробувань стає як завгодно малою ) ;
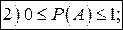 Дійсно:
Дійсно: 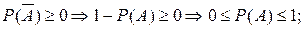
3) Теорема додавання ймовірностей. Для будь-яких подій A та B справедливе співвідношення
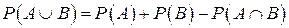 . .
| (3) | ||
Доведення. Подамо події A+B та B у вигляді суми попарно несумісних подій (рис.1.4) 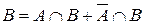 , , 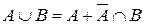 . Тоді на підставі аксіоми 3 одержимо P(AÈB)=P(A) . Тоді на підставі аксіоми 3 одержимо P(AÈB)=P(A) 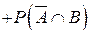 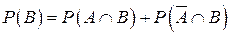 . Підставляючи вираз . Підставляючи вираз
| 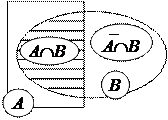 Рис. 1.4
Рис. 1.4
| ||
P( 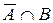 ) із другого співвідношення в перше, приходимо до рівності (2).
) із другого співвідношення в перше, приходимо до рівності (2).
Між іншим, з (3) випливає, якщо Р(А) +Р(В)> 1, то Р(А 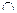 В) >0 і, отже,події А та В є сумісними .
В) >0 і, отже,події А та В є сумісними .
Дата добавления: 2016-10-17; просмотров: 2028;
