Формула повної ймовірності
Нехай є n припущень (гіпотез) Hk (k=1,...,n) щодо умов проведення випробування, з яким пов’язана подія А. При цьому із тих чи інших міркувань відомі ймовірності P(Hk), P(A/Hk). Як можна прогнозувати спроможність появи події А?
Теорема. Нехай події Hk (k=1,...,n) складають повну систему. Тоді для будь-якої події A справедлива рівність
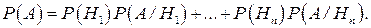 (4) (4)
| 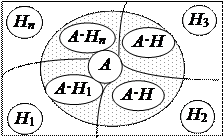 Рис. 1.5
Рис. 1.5
|
Доведення. Оскільки W=H1ÈH2È...ÈHn, то подію A можна представити у вигляді суми попарно несумісних подій
A = A·H1ÈA·H2È...ÈA·Hn
рис.1.5). Послідовно застосовуючи теореми додавання та множення ймовірностей (формулу 3 з аксіом ймовірності розділу 1.2 та формулу (2) розділу 1.3), одержимо:
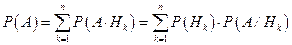 .
.
Якщо P(А 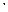 Hi)=0, то відповідна складова у сумі повинна бути пропущена.
Hi)=0, то відповідна складова у сумі повинна бути пропущена.
Приклад 1.Футбольна команда грає за схемою 1-4-2-4. Ймовірність забити пенальті для нападника 0.8, півзахисника 0.7, захисника 0.6, вратаря 0.5. Знайти ймовірність того, шо навмання обраний ігрок забиває пенальті.
Розв’язання. Нехай подія А –навмання обраний ігрок забиває пенальті. Призначимо гіпотези:
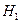 – вибір нападника;
– вибір нападника; 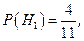
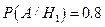
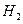 – вибір півзахисника,
– вибір півзахисника, 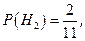
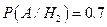
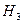 – вибір захисника;
– вибір захисника; 
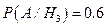
 – вибір вратаря .
– вибір вратаря . 
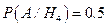 . За формулою повної ймовірності, маємо
. За формулою повної ймовірності, маємо
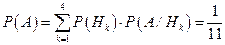 (4
(4  0.8+2
0.8+2  0.7+4
0.7+4  0.6+1
0.6+1  0.5)=
0.5)= 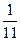 (3.2+1.4+2.4+0.5)=
(3.2+1.4+2.4+0.5)= 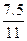 =0.68.
=0.68.
1.3.3. Теорема гіпотез (формули Бейєса)
Ця теорема є наслідком формули повної ймовірності..
Теорема. Нехай події Hk (k=1,...,n) утворюють повну систему подій (P(Hk)>0). Тоді для будь-якої події A (P(A)>0), що настала у наслідку проведення випробувань, виконується співвідношення
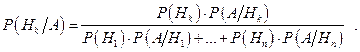
| (5) |
Доведення. Оскільки 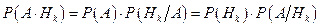 , то на підставі формули (5) одержимо
, то на підставі формули (5) одержимо
 .
.
Події Hk прийнято називати гіпотезами, P(Hk) - апріорними (відомими до проведення випробування), а P(Hk/A) - апостеріорними (обчисленими після випробування) ймовірностями цих гіпотез. Формула (7) показує, як треба переоцінити ймовірності здійснення кожної гіпотези, якщо подія А настала.
Дата добавления: 2016-10-17; просмотров: 679;
