Асимптотичні формули для схеми Бернуллі
Формула (1) приводить до громіздких обчислень при великих значеннях n і k, а також при малих значеннях p або 1– p. Тому, доцільно мати наближені, але прості формули для розрахунку відповідних ймовірностей ,або їх сум..
1) Формули Муавра-Лапласа. Локальна формула :
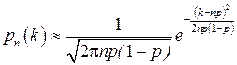 . .
| (2) |
має місце при p і 1-p істотно відмінних від 0 і великих значеннях n і k . Відносна похибка цієї формули зменшується при зростанні n і зменшенні |k-np|. Вона застосовується звичайно при  n >100, np(1– p)>20 і |k- np |< <3
n >100, np(1– p)>20 і |k- np |< <3 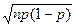 .
.
Приклад. Знайти ймовірність того, що подія А настане k=85 раз при n=400 випробуваннях, якщо ймовірність появи події А в кожному випробуванні дорівнює p=0.2.
Розв’язання. n=400, p=0.2. np=400 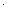 0.2=80, np(1– p)=80
0.2=80, np(1– p)=80 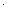 0.8=64,
0.8=64, 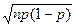 =8,
=8, 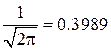 ,
,
k-np=85-80=5, 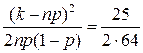 ,
, 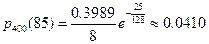
Інтегральна формула:
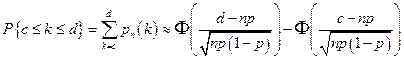 . .
| (3) |
де 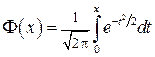 так звана функція Лапласа (або інтеграл помилок). Значення цієї непарноїфункції наведені в таблиці 1 додатка, а її графік на рис. 1.17. Формула (4) є твердженням теореми Муавра-Лапласа з пункту 3.2.4. Вона використовується тоді, коли і формула (3 )
так звана функція Лапласа (або інтеграл помилок). Значення цієї непарноїфункції наведені в таблиці 1 додатка, а її графік на рис. 1.17. Формула (4) є твердженням теореми Муавра-Лапласа з пункту 3.2.4. Вона використовується тоді, коли і формула (3 )
.
Приклад 2.Гральний кубик підкидається 1200 раз. Знайти ймовірність того, що кількість випадань одиниці знаходиться в діапазоні між 195 та 210 включно.
Розв’язання.Оскільки n=1200, p=1/6, то маємо 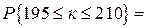 = = 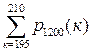 = = 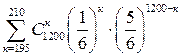 .
Подальше обчислення пов’язане з великими труднощами. Тому скористаємося формулою (3). Оскільки np=200, .
Подальше обчислення пов’язане з великими труднощами. Тому скористаємося формулою (3). Оскільки np=200, 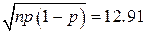 , d– np =10, c– np = – 5, шукана ймовірність приблизно дорівнюватиме , d– np =10, c– np = – 5, шукана ймовірність приблизно дорівнюватиме
|
|
Рис.1.7
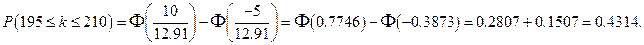
Дата добавления: 2016-10-17; просмотров: 1252;

