Неперервні випадкові величини
Означення 1. Випадкова величина X називається неперервною, якщо її функція розподілу неперервна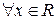 
та диференційовна всюди окрім, можливо, окремих точок.
Функція розподілу на рис 2.4 не диференційовна в точках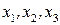 
. Неперервна ВВ 
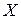визначається за допомогою іншої функції 
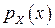, яка називається щільністю розподілу ймовірностей (або щільністю ймовірності) ВВ X.
Означення 2.. Випадкова величина X називається неперервною, якщо існує така невідємна функція
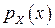, яка називається щільністю розподілу ВВ Х, що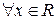
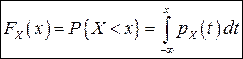(1)
Властивості щільності ймовірності :
1.  ,
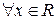2. 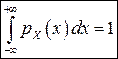 – умова нормування (2)
3. 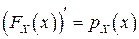 .в точках неперервності
| 
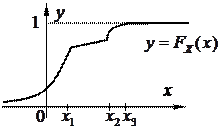Рис. 2.4
|
функції pX (x)
4. Ймовірність попадання неперервної випадкової величини X у проміжок [c; d) знаходиться за формулою
 .
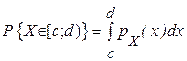| (3) |
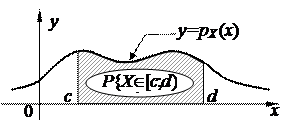
| Геометричний зміст цієї властивості (площа криволінійної трапеції) дає рис. 2.5. У лівій частині формули (3) можна замінити проміжок [c; d) на [c; d], (c; d). | Рис. 2.5 |
Приклад 1. Щільність ймовірності неперервної ВВ X має вигляд
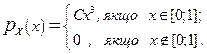
Знайти: 1) С; 2) FX (x); 3) P{XÎ[1 ∕ 3; 4]} .
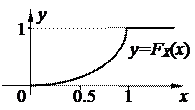Розв’язання. 1) Коефіцієнт С знаходимо із умови нормування:
 .
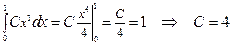2) 
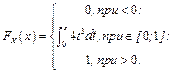
| Рис.2.6 |
Графік функції розподілу приведено на рис.2.7.
3) 
.
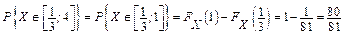Дата добавления: 2016-10-17; просмотров: 729;