Функція розподілу випадкового вектора
Якщо результат випробування визначається сукупністю випадкових величин Х1, Х2 ,…, Хn , то будемо розглядати їх як координати n-вимірного випадкового вектора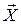 
(X1;…; Xn). Отже, під n- вимірним випадковим вектором розуміють упорядковану сукупність n випадкових величин. Виявляється, що для повного опису випадкового вектора (ВВ-ра) потрібно мати не тільки інформацію про властивості його координат, але і про їх взаємодію.
Наведемо приклади ВВ-в: 1) точка потрапляння у плоску мішень характеризується випадковим вектором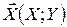 
, де X та Y координати точки потрапляння в системі координат, розміщеній в площині мішені; 2) місце розташування літака за допомогою системи радіонавігації описується тривимірним
У подальшому найчастіше мова йтиме про двовимірний випадковий вектор .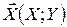
Функцією розподілу двовимірного випадкового вектора 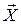(X;Y) називається задана у площині xOy функція 
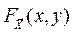така, що
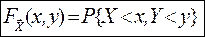. (1)
| |
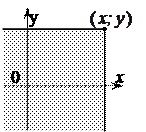
З геометричної точки зору функція розподілу 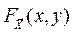дорівнює ймовірності потрапляння точки (X; Y) у нескінченний прямокутник з вершиною в точці 
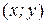, який розташовано зліва та нижче цієї точки (рис. 2.20). Відзначимо деякі властивості двовимірної функції розподілу:
| Рис.2.20 |
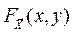є не спадною, неперервною зліва по кожному аргументу;
2) 3) |
, 
, 
;
, 
.Дата добавления: 2016-10-17; просмотров: 481;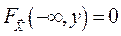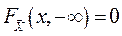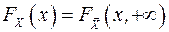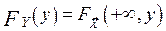