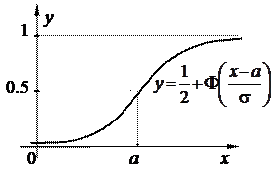Основні неперервні закони розподілу.
Розглянемо деякі найбільш важливі неперервні розподіли.
1)Рівномірний (прямокутний) розподіл. Випадкова величина X рівномірно розподілена у проміжку [c ; d], якщо її щільність ймовірності має вигляд (рис.2.8, а):
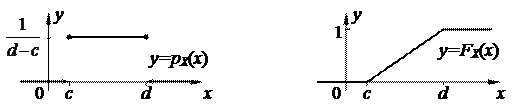
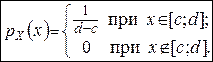 (1)
(1)
| а Рис. 2.8 б |
Цей розподіл є неперервним аналогом класичного означення ймовірності (відповідає припущенню про рівноможливій вибір точки у проміжку [c;d]). А саме, нехай [с1;d1] 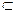 [c;d] . Тоді Р{X
[c;d] . Тоді Р{X 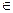 [c1;d1]} =
[c1;d1]} = 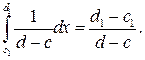
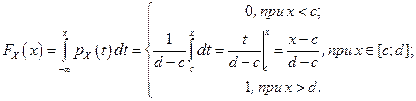 (2)
(2)
Графік функції розподілу приведено на рис.2.8, б.
Математичне сподівання ВВ Х за теоремою 1 підрозд. 2.1.4.2 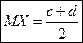 (3) а дисперсія за формулою (1)підрозд.2.1.4.4
(3) а дисперсія за формулою (1)підрозд.2.1.4.4 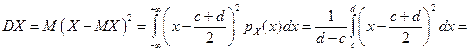
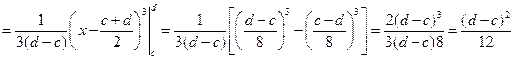 , Отже,
, Отже, 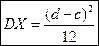 (4). Якщо шкала приладу має ціну поділці
(4). Якщо шкала приладу має ціну поділці 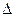 і відлік робиться з точністю до цілої поділці шкали, то похибка вимірювання є неперервною випадковою величиною, яка рівномірно розподілена у проміжку
і відлік робиться з точністю до цілої поділці шкали, то похибка вимірювання є неперервною випадковою величиною, яка рівномірно розподілена у проміжку
[– 0.5∆ ; 0.5∆].
Помилка, яка допускається при округленні числа з точністю до 10-m, рівномірно розподілена у проміжку [– 0.5·10-m ; 0.5·10-m].
Приклад 1.Потяги метройдуть з інтервалом 4.5хв. Пасажир виходить на платформу у випадковий момент часу. Знайти; а) МХ та 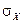 ВВ часу очікування поїзда; б)ймовірність того, що пасажир буде очікувати поїзд не більше 3-х хвилин; в) не більше 4-х.
ВВ часу очікування поїзда; б)ймовірність того, що пасажир буде очікувати поїзд не більше 3-х хвилин; в) не більше 4-х.
Розв’язання . Оскільки ВВ Х час очікування потяга має щільність розподілу 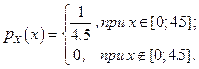 , з функцією розподілу
, з функцією розподілу 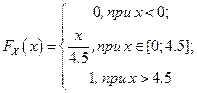 , то за формулою
, то за формулою
P{XÎ[а; b)} = FX (b) – FX (a) одержимо, що P{XÎ[0; 3)} = FX (3) – FX (0)= 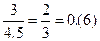 , а
, а
P{XÎ[0; 4)} = FX (4) – FX (0)= 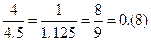 , За формулами (3), (4) МХ=2.25.
, За формулами (3), (4) МХ=2.25. 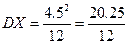 ,
,
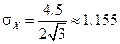
2) Показниковий розподіл. Випадкова величина X має показниковий розподіл з параметром l>0, якщо її щільність розподілу
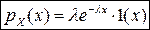 , (5)
, (5)
де 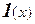 =
= 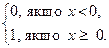 – так звана одинична функція Хевісайда.
– так звана одинична функція Хевісайда.
Відповідна функція розподілу має, на підставі (1) підрозд. 2.1.3, вигляд

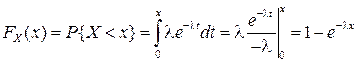 (x
(x 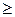 0) .
0) .
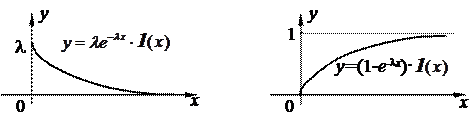 Таким чином, P{X
Таким чином, P{X 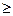 h}=1–P{0
h}=1–P{0 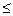 X< h}=1–FX(h) =1–(1–e-λh )= e-λh .
X< h}=1–FX(h) =1–(1–e-λh )= e-λh .
| а Рис. 2.9 б |
Графіки щільності ймовірності та функції розподілу приведені на рис.2.9, а і 2.9, б.
Запис X~Е( 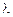 ) означає, що ВВ Х розподілена за показниковим законом з параметром
) означає, що ВВ Х розподілена за показниковим законом з параметром 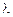 .
.
В теорії масового обслуговування (див. підпункт 3.4.1.1)припускається, що час обслуговування Тобсл підкоряється показниковому закону 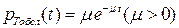 .
.
Приклад 2.Нехай кількість відмов приладу на проміжку часу [0 ; t) розподілена за законом Пуассона з параметром lt
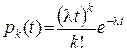 ( (  =0,1,2,…) , =0,1,2,…) ,
|  Рис. 2.10
Рис. 2.10
|
а ВВ T – тривалість проміжку часу між двома послідовними відмовами приладу (рис.2.10). Знайти закон розподілу ВВ T .
Розв’язання. Оскільки подія T ³ t означає, що на проміжку [0 ; t) прилад працює безвідмовно, то P{T ³ t} = p0(t) =e–λt. Отже,
FT (t) =P{T< t} =1– Р{T ≥ t} =1– e–λt
і, таким чином,
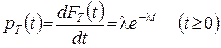 .
.
Звідси випливає, що тривалість проміжку часу між двома послідовними відмовами приладу розподілена за показниковим законом з параметром l.
Для показникового закону 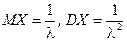
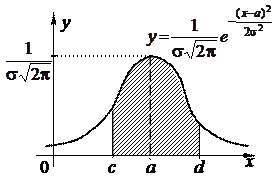
3)Нормальний розподіл (розподіл Гаусса). Випадкова величина X має нормальний розподіл з параметрами a та s2, якщо її щільність розподілу ймовірностей має вигляд (рис.2.12, а):
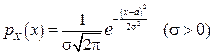 . .
| (13) |
Дослідимо функцію 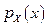 .1.
.1. 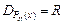 2.
2.  як показникова функція.
як показникова функція.
3. 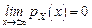 .4. Екстремум;
.4. Екстремум; 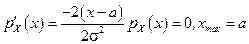
У подальшому запис X~N(a;s2) означатиме, що ВВ X має розподіл Гаусса з параметрами a та s2. Графік розподілу Гаусса є симетричним відносно прямої x=a. Єдиний максимум досягається при x=a і дорівнює 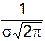 . Оскільки площа під графіком дорівнює 1, то при зменшенні s графік стає більш «високим» та «вузьким».
. Оскільки площа під графіком дорівнює 1, то при зменшенні s графік стає більш «високим» та «вузьким».
Первісна від нормальної щільності 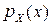 не виражається явно через елементарні функції. Функція розподілу випадкової величини X~N(a;s2) виражається через функцію Лапласа Ф(x) (формула (5) розділу 1.5). Дійсно,
не виражається явно через елементарні функції. Функція розподілу випадкової величини X~N(a;s2) виражається через функцію Лапласа Ф(x) (формула (5) розділу 1.5). Дійсно,
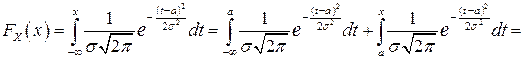
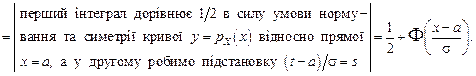
Графік функції розподілу приведено на рис.2.12, б.
а Рис. 2.12 б |
Розподіл Гаусса відіграє фундаментальну роль в застосуваннях теорії ймовірності.
Оскільки ймовірність потрапляння ВВ 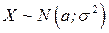 у проміжок дорівнює різниці значень функції розподілу на кінцях проміжку, то
у проміжок дорівнює різниці значень функції розподілу на кінцях проміжку, то
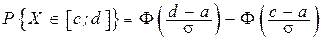 . .
| (14) |
Якщо проміжок [c; d] довжиною 2ss розташований симетрично відносно точки x=a, то формула (14) набирає особливо простого вигляду
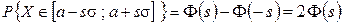 . (
. ( 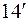 )
)
Зокрема: 1) ймовірність попадання у проміжок [a-3s; a+3s] дорівнює 2Ф(3) = 0.9973. Таким чином, можна стверджувати, що подія {XÏ[a-3s; a+3s]} є практично неможливою (при одному випробуванні отримати значення, яке відхиляється від а більше, ніж на 3s неможливо) . У цьому полягає знамените правило «трьох сигм»;
2) 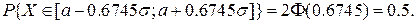 Отже, події
Отже, події
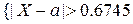 σ}, {|X–a|<0.6745σ} є рівноймовірними. Величина Е=0.6745σ називається серединним або імовірнимвідхиленням.
σ}, {|X–a|<0.6745σ} є рівноймовірними. Величина Е=0.6745σ називається серединним або імовірнимвідхиленням.
Приклад 6. Відхилення розміру деталі від стандартного розподілено за законом N(0;16 мм2). Деталь вважається придатною, якщо відхилення від стандарту не перевищує 6 мм. 1) Який відсоток випуску непридатних деталей? 2)Яким має бути σ , щоб при відхиленні від стандарту 3 мм ймовірність придатності деталі була не менш , ніж 0.95 ?
Розв’язання. Нехай ВВ X – відхилення розміру деталі від номінального. 1) Знайдемо ймовірність того, що деталь буде забраковано
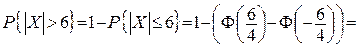
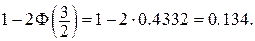
Таким чином, брак складає майже 13.5%.
2) 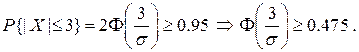 За таблицею функції Лапласа маємо
За таблицею функції Лапласа маємо 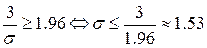 мм.
мм.
Випадкові вектори
Дата добавления: 2016-10-17; просмотров: 879;