Дисперсія випадкової величини та її властивості
Після того, як математичне сподівання ВВ знайдено, виникає питання, наскільки сильно значення ВВ відхиляється від математичного сподівання. Характеристикою міри розсіювання ВВ навколо математичного сподівання є математичне сподівання квадрата флуктуації
Означення 1. Дисперсією випадкової величини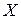 
(позначається 
або 
) називається невід’ємне число, яке дорівнює математичному сподіванню квадрата флуктуації цієї величини:
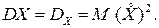(1)
Розмірність дисперсії дорівнює квадрату розмірності ВВ 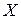. Тому зручно з практичної точки зору приймати як міру розсіювання ВВ середнє квадратичне (стандартне) відхилення 
, вимірність якого співпадає з вимірністю ВВ .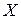
Чим менше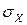 
( ), тим тісніше групуються значення випадкової величини навколо її математичного сподівання.
При знаходженні дисперсії, як правило, використовують не формулу (1), а інший вираз, який одержується з правої частини цієї формули на підставі властивостей математичного сподівання:
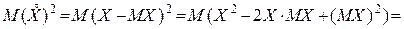
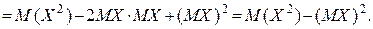
Таким чином, 
Запишемо формулу (2) у розгорнутому вигляді
(3)
Приклад 5Знайти: а)DX та 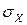для дискретної ВВ Х з прикладу 1;б)DX для неперервної ВВ Х з
| X | -1 | ||
| P | 0.2 | 0.5 | 0.3 |
прикладу 2Розв’язання.а) З результатів прикладів 1,3: МХ =1.7,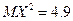 
, 
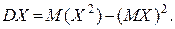DX = 4.9-2.89 = 2.01.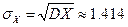 
б)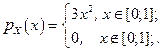 
З результатів прикладів 2,4: 
, 
, 
.. 
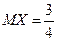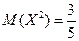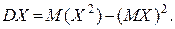
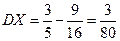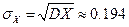
Дата добавления: 2016-10-17; просмотров: 723;