Дискретний випадковий вектор
Якщо обидві координати вектора 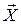 є дискретними випадковими величинами, то вектор
є дискретними випадковими величинами, то вектор 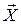 називають дискретним випадковим вектором. Дискретний ВВ-р задається набором значень (xk; yj) та ймовірностями pkj=P{X=xk,Y=yj}, з якими ці значення приймаються. Ясно, що сума всіх ймовірностей pkj дорівнює одиниці.
називають дискретним випадковим вектором. Дискретний ВВ-р задається набором значень (xk; yj) та ймовірностями pkj=P{X=xk,Y=yj}, з якими ці значення приймаються. Ясно, що сума всіх ймовірностей pkj дорівнює одиниці.
Дискретний ВВ-р, як правило, задають таблицею розподілу.
| Y X | y1 | y2 | ... | ym |
| x1 | p11 | p12 | ... | p1m |
| x2 | p21 | p22 | ... | p2m |
| ... | ... | ... | ... | ... |
| xn | pn1 | pn2 | ... | pnm |
У таблиці розподілу дискретного ВВ-ра міститься вся інформація про нього. Зокрема, ця таблиця дозволяє знайти закони розподілу координат вектора.
Дійсно,оскільки подія {X=xk} складається з суми попарно несумісних подій {X=xk,Y=y1}, {X=xk,Y=y2},..., {X=xk,Y=ym}, то щоб одержати ймовірність pk =Р{X=xk} потрібно просумувати ймовірності pkj, які стоять у k-му рядку таблиці розподілу:
| pk = P{X=xk} = pk1+ pk2+...+pkm. | (2) |
Аналогічно, щоб одержати ймовірність P{Y=yj} потрібно просумувати ймовірності pkj , які стоять у j-ому стовпцю таблиці розподілу:
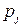 =P{Y=yj}=p1j +p2j +…+pnj . =P{Y=yj}=p1j +p2j +…+pnj .
| ( 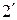 ) )
|
| Y X | -2 | -1 | |
| 0.15 | 0.05 | 0.25 | |
| 0.35 | 0.2 |
Приклад 1. Знайти: а) розподіл координат дискретного ВВ-ра 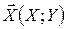 , заданого таблицею розподілу; б) знайти ймовірності: P{X=1,Y<0}, P{X<0.5,Y>–1.5}, P{X+Y>0}.
, заданого таблицею розподілу; б) знайти ймовірності: P{X=1,Y<0}, P{X<0.5,Y>–1.5}, P{X+Y>0}.
Розв’язання. а) На підставі формул (2) ,( 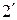 ) одержуємо розподіли координат X та Y:
) одержуємо розподіли координат X та Y:
| X | Y | -2 | -1 | ||||
| P | 0.45 | 0.55 | P | 0.5 | 0.25 | 0.25 |
б)P{X=1,Y<0}=0.35+0.2=0.55, P{X<0.5,Y>-1.5}=0,05+0.25=0.3,
P{X+Y>0}=0.25.
Виникає запитання: коли можливо за розподілом координат знайти розподіл вектора?
Приклад 2.Знайти розподіл координат дискретного ВВ-ра 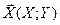 ,який
,який
| Y X | –2 | -1 | |
| 0.15 | 0.15 | 0.15 | |
| 0.35 | 0.1 | 0.1 |
заданий таблицею розподілу ймовірностей
Розв’язання.На підставі формул (2), ( 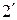 ) одержуємо розподіли координат X та Y
) одержуємо розподіли координат X та Y
| X | Y | -2 | -1 | ||||
| P | 0.45 | 0.55 | P | 0.5 | 0.25 | 0.25 |
Отже, розподіли координат X та Y співпадають з розподілами координат з
приклада 1, хоча розподіли векторів 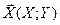 відрізняються.
відрізняються.
Введемо подібно до умовної ймовірності події поняття умовного розподілу координати X дискретного ВВ-ра 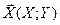 за умови , що його координата Y=
за умови , що його координата Y= 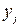
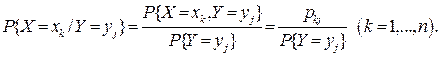 (3)
(3)
Зрозуміло, що 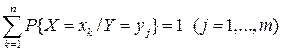 .
.
Аналогічно визначається умовний розподіл випадкової величини Y за умови , що випадкова величина 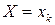 .
.
Означення 1.Дискретні випадкові величини X та Y називаються незалежнимитоді, коли при всіх значеннях k та j є справедливими співвідношення
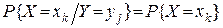 . (4)
. (4)
Випадкові величини X та Y незалежні тоді і тільки тоді, коли при всіх значеннях k та j виконується рівність
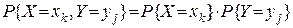 . (5)
. (5)
Іншими словами, двовимірний розподіл дискретного вектора відновлюється по одновимірних розподілах його координат лише у тому випадку, коли координати вектора є незалежними випадковими величинами.
Приклад 3. В умовах прикладу 1 знайти умовні розподіли 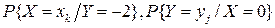 та з’ясувати питання про те, чи є випадкові величини X та Y залежними.
та з’ясувати питання про те, чи є випадкові величини X та Y залежними.
Розв’язання. На підставі формули (3) знайдемо умовний розподіл випадкової величини X при Y= –2:
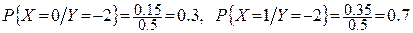 .
.
Аналогічно одержуємо умовний розподіл випадкової величини Y за умови, що випадкова величина X =0:
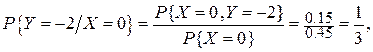
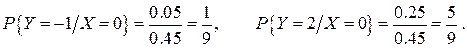
Випадкові величини X та Y є залежними, наприклад, тому що Випадкові величини X та У є залежними, наприклад, тому що 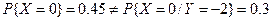 .
.
Дата добавления: 2016-10-17; просмотров: 1231;
