Базис и размерность линейного пространства. Координаты вектора в данном базисе

Определение 10.Векторы 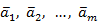называются линейно зависимыми, если существуют такие числа 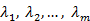, не равные одновременно нулю, что

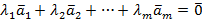. (1)

Если равенство выполняется только при 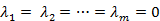, то векторы 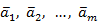называются линейно независимыми.

Пример.Система векторов 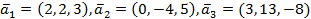линейно зависима, так как .

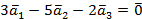Определение 11.Векторы 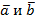называются коллинеарными, если они параллельны одной прямой, т.е. 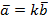или .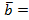

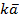Утверждение.Система, содержащая два вектора 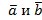, линейно зависима в том и только том случае, когда эти векторы коллинеарны.

Доказательство. Если оба вектора равны нулю, то они, очевидно, линейно зависимы и коллинеарны. Пусть 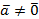. Допустим сначала, что векторы 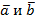линейно зависимы. Тогда 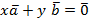для некоторых x и y, не равных нулю одновременно. Если 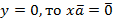. Но тогда и 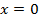, т.к. 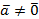. Если же 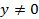, то 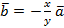. Предположим теперь, что векторы коллинеарны, т.е. 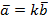. Т.к. их линейная комбинация 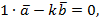то векторы 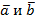линейно зависимы.

Определение 12.Три вектора 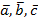в R³, лежащие в одной плоскости или параллельные одной плоскости, называются компланарными.

Упражнение.Доказать, что три вектора в R³ линейно зависимы в том и только том случае, когда они компланарны.