Свойства векторов линейного пространства
1. Если среди векторов 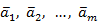 имеется нулевой вектор, то эти векторы линейно зависимы.
имеется нулевой вектор, то эти векторы линейно зависимы.
Доказательство. Если, например, 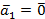 , то равенство (*) справедливо при
, то равенство (*) справедливо при 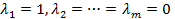 и, следовательно, эти векторы линейно зависимы.
и, следовательно, эти векторы линейно зависимы.
2. Система, содержащая более одного вектора, линейно зависима в том и только том случае, когда среди данных векторов имеется такой, который линейно выражается через остальные.
Доказательство. Пусть среди данных векторов 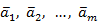 имеется, например, вектор
имеется, например, вектор 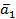 , который линейно выражается через остальные
, который линейно выражается через остальные
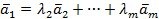 .
.
Прибавляя к обеим частям равенства вектор 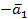 , получим
, получим
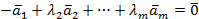 ,
,
Т.е. линейная комбинация векторов равна нулю, причём имеются коэффициенты, не равные нулю. Следовательно, система векторов линейно зависима.
Обратно, пусть векторы линейно зависимы, т.е. имеет место равенство (*) с не равными нулю одновременно коэффициентами 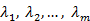 . Например,
. Например, 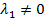 . Перепишем равенство (*) в виде
. Перепишем равенство (*) в виде
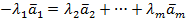 .
.
Разделим обе части равенства на 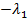 . Получим, что
. Получим, что 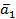 линейно выражается через остальные векторы системы
линейно выражается через остальные векторы системы
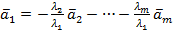 ,
,
3. Если часть системы линейно зависима, то и вся система линейно зависима.
Доказательство. Действительно, если, например, векторы 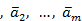 линейно зависимы, то справедливо равенство
линейно зависимы, то справедливо равенство
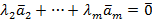 ,
,
в котором не все числа 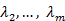 равны нулю. Но тогда с теми же числами и
равны нулю. Но тогда с теми же числами и 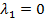 справедливо равенство (*).
справедливо равенство (*).
4. Система из одного вектора { 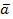 } линейно зависима тогда и только тогда, когда вектор
} линейно зависима тогда и только тогда, когда вектор 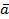 нулевой.
нулевой.
Доказательство. Пусть система, состоящая из одного вектора 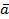 , линейно зависима, тогда найдётся число
, линейно зависима, тогда найдётся число 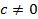 такое, что
такое, что 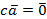 . Умножим обе части равенства на c-1. Получим
. Умножим обе части равенства на c-1. Получим 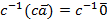 или
или 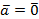 .
.
Обратно, если 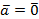 , то очевидное равенство
, то очевидное равенство 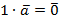 показывает, что система векторов {
показывает, что система векторов { 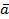 } линейно зависима.
} линейно зависима.
Определение 13.Линейное пространство Rп называется п - мерным, если в нём существует п линейно независимых векторов, а любые из (п + 1) векторов уже являются зависимыми. Размерность пространства – это максимальное число содержащихся в нём линейно независимых векторов. Число п называется размерностью пространства Rп и обозначают dim ( Rп ).
Определение 14.Система векторов из Rп называется базисом пространства в Rп, если:
1. эти векторы линейно независимы;
2. любой вектор из Rп является линейной комбинацией векторов данной системой.
Следовательно, базисом на плоскости будут любые два неколлинеарных вектора, а в пространстве – любые три некомпланарных вектора.
Теорема.Линейно независимая система векторов в Rп тогда и только тогда является базисом, когда их число равно п.
Теорема.Каждый вектор 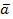 линейного пространства R можно представить (и при том единственным способом) в виде линейной комбинации векторов базиса.
линейного пространства R можно представить (и при том единственным способом) в виде линейной комбинации векторов базиса.
Доказательство. Пусть векторы 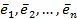 образуют произвольный базис п-мерного пространства Rп . Так как любые из (п+1) векторов п-мерного пространства Rп зависимы, то будут зависимы, в частности, векторы
образуют произвольный базис п-мерного пространства Rп . Так как любые из (п+1) векторов п-мерного пространства Rп зависимы, то будут зависимы, в частности, векторы 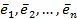 и рассматриваемый вектор
и рассматриваемый вектор 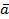 . Тогда существуют такие не равные одновременно нулю числа
. Тогда существуют такие не равные одновременно нулю числа  , что
, что
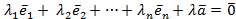 .
.
При этом 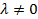 , ибо в противном случае, если
, ибо в противном случае, если 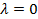 и хотя бы одно из чисел
и хотя бы одно из чисел 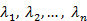 было бы отлично от нуля, то векторы
было бы отлично от нуля, то векторы 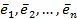 были бы линейно зависимы. Следовательно,
были бы линейно зависимы. Следовательно,
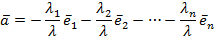
или
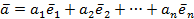 ,
,
где 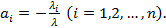
Предположим, что существует два разложения 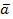 по базису
по базису 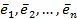 в Rп, т.е.
в Rп, т.е.
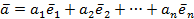 ,
,
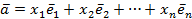 .
.
Вычтем одно равенство из другого
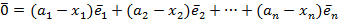 .
.
Поскольку это базис, то все коэффициенты равны нулю, т.е. 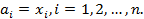
Определение. Размерность линейной оболочки 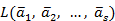 векторов называется рангом системы векторов
векторов называется рангом системы векторов 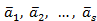 .
.
Таким образом, ранг системы равен r, если среди векторов системы существует r линейно независимых, а любые q > r векторов данной системы линейно зависимы. Ранг же линейно независимой системы равен числу её членов.
Подсистема 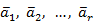 системы векторов
системы векторов 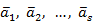 называется базисом этой системы, если она является базисом линейной оболочки
называется базисом этой системы, если она является базисом линейной оболочки 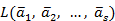 .
.
Дата добавления: 2016-10-17; просмотров: 1428;
