Ранг матрицы и элементарные преобразования

Матрицу размера 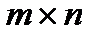можно рассматривать как систему, состоящую из т векторов-строк (векторов пространства 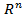), или как систему, состоящую из п векторов-столбцов (векторов пространства ).

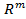Определение 5. Рангом системы строк (столбцов) матрицы 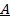, содержащей 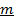строк и 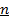столбцов называется максимальное число линейно независимых строк (столбцов).

Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие.

Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.

Из определения следует, что ранг матрицы размера 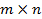есть целое число, заключенное в пределах от 0 до т. Причём r(A) = 0 только лишь в том случае, когда A = 0.

Элементарными преобразованиями над строками матрицы называется любое из следующих действий:

1. Вычеркивание нулевой строки (если таковая имеется)

2. Перестановка строк

3. Умножение любой строки на число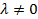

4. Прибавление к одной из строк другой строки, умноженной на любое число.

Лемма. Ранг матрицы не меняется при элементарных преобразованиях.

Определение 6.Матрица А называется ступенчатой, если она имеет вид

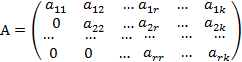
Ранг ступенчатой матрицы равен r , т.к. имеется r линейно независимых вектор-строк матрицы А (Утверждение.Лестничная система векторов линейно независима).

Ранг матрицы вычисляется путём приведения к её к ступенчатому виду

Пример.Найти ранг матрицы А.

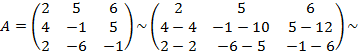
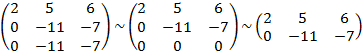
Т.к. в матрице ступенчатого вида осталось 2 строки, то ранг равен 2.