Умножение матриц. Обратная матрица
Определение 7.Умножение матрицы 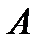 на матрицу
на матрицу 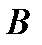 определено, когда число столбцов первой матрицы равно числу строк второй (условие согласованности). Тогда произведением матриц
определено, когда число столбцов первой матрицы равно числу строк второй (условие согласованности). Тогда произведением матриц 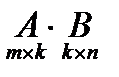 называется матрица
называется матрица 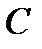 , каждый элемент которой
, каждый элемент которой 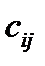 равен сумме произведений элементов
равен сумме произведений элементов 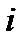 -ой строки матрицы
-ой строки матрицы 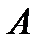 на соответствующие элементы
на соответствующие элементы 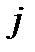 -го столбца матрицы
-го столбца матрицы 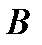 :
:
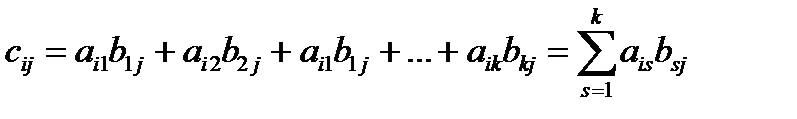 , где
, где 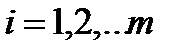 ,
, 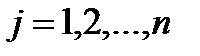 .
.
Пример. Вычислить произведение матриц 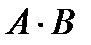 , где
, где
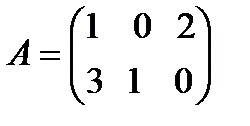 ,
, 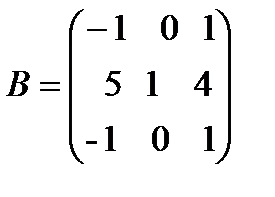 .
.
Решение. Найдем размер матрицы произведения  , следовательно, умножение возможно.
, следовательно, умножение возможно.
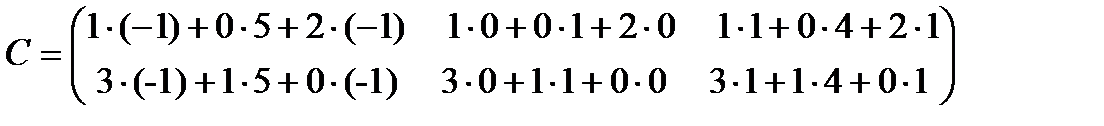 =
= 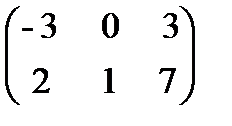 .
.
Определение 8. Матрица 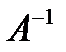 называется обратной по отношению к квадратной матрице
называется обратной по отношению к квадратной матрице 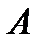 , если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица:
, если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица:
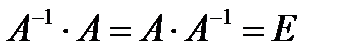 .
.
Нахождение обратной матрицы с помощью элементарных
Преобразований.
Пусть А – невырожденная матрица. Припишем к ней (например, справа) единичную матрицу Е. Далее с помощью элементарных преобразований над строками «сдвоенной матрицы (А│E) приводим А («левую половину») к единичной матрице Е. Тогда на месте первоначально приписанной матрицы Е окажется матрица А-1 .
Заметим, что из самого способа нахождения матрицы А-1 легко следует, что матрица, обратная для А-1, есть А. Действительно, проделав преобразования, переводящие А в Е, в обратном порядке, из матрицы Е получим А, а из А-1 матрицу Е. это означает, что А есть обратная матрица для А-1, т.е. А-1А = Е.
Пример.Для матрицы
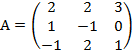
Найти обратную матрицу А-1 .
Решение. Составим матрицу
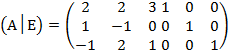 .
.
С помощью элементарных преобразований приведём её левую «половину» А к матрице Е:
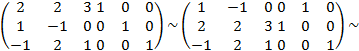
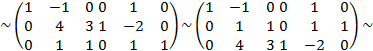
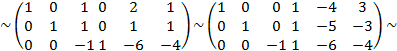
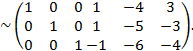
Правее вертикальной черты получилась обратная матрица А-1:
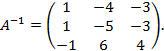
Способ решения уравнения АХ = В
Пусть А – невырожденная матрица. Приведём её с помощьюэлементарных преобразований над строками к единичной матрице Е. Если затем те же самые преобразования применить к строкам матрицы В, то получим искомую матрицу Х.
Заметим, что нет необходимости специально запоминать преобразования, совершенные над А, чтобы проделать их над В. Вместо этого можно приписать к А (например, справа) матрицу В
(А|В)
и выполнять преобразования сразу над «сдвоенной» матрицей. После того как левая половина приведётся к Е, правая приведётся к искомой матрице Х.
Пример. Решить уравнение
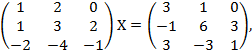
где Х – неизвестная матрица 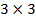 .
.
Решение. Имеем
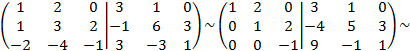
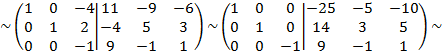
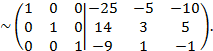
Правее вериткальной черты получилась искомая матрица
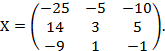
Дата добавления: 2016-10-17; просмотров: 907;
