Ортогональный и ортонормированный базисы
Определение 17.Два вектора называются ортогональными, если их скалярное произведение равно нулю.
Векторы 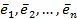 п – мерногоевклидова пространства образуют ортогональный базис, если эти векторы попарно ортогональны, т.е.
п – мерногоевклидова пространства образуют ортогональный базис, если эти векторы попарно ортогональны, т.е. 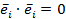 при
при 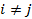 , и ортонормированный базис, если эти векторы попарно ортогональны и модуль каждого из них равна единице.
, и ортонормированный базис, если эти векторы попарно ортогональны и модуль каждого из них равна единице.
Теорема.Во всяком п – мерном евклидовом пространстве существует ортонормированный базис.
Доказательство. В качестве обоснования теоремы представим алгоритм последовательного построения ортонормированного базиса по заданному базису 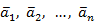 , называемый процессом ортогонализации Грама-Шмидта.
, называемый процессом ортогонализации Грама-Шмидта.
Пусть вектор 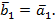 Найдём нормированный вектор
Найдём нормированный вектор 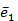 (для которого
(для которого 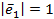 ) делением
) делением 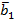 на его норму
на его норму 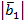 , т.е.
, т.е. 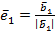 , и получим первый вектор ортонормированного базиса. Построим вектор
, и получим первый вектор ортонормированного базиса. Построим вектор
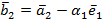 ,
,
так, чтобы он был ортогонален вектору 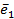 , т.е. скалярное произведение
, т.е. скалярное произведение 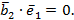 Для нахождения
Для нахождения 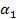 умножим скалярно полученное равенство на
умножим скалярно полученное равенство на 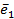 ; получим, используя свойство скалярного произведения:
; получим, используя свойство скалярного произведения:
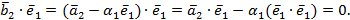
Учитывая, что 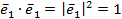 , найдём
, найдём 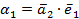 . Это означает, что вектор
. Это означает, что вектор 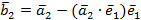 будет ортогонален вектору
будет ортогонален вектору 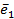 , и вторым вектором ортонормированного базиса станет нормированный вектор
, и вторым вектором ортонормированного базиса станет нормированный вектор 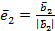 .
.
Используя полученные векторы 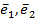 и заданный вектор
и заданный вектор 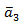 , построим вектор
, построим вектор
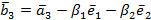 ,
,
ортогональный единичным векторам 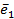 и
и 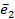 , для чего умножим скалярно равенство последовательно на
, для чего умножим скалярно равенство последовательно на 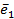 и
и 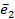 и приравняем его к нулю:
и приравняем его к нулю:
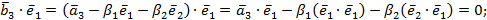
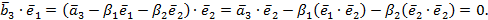
Т.к. скалярные произведения ортонормированных векторов
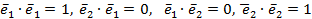 ,
,
то получим 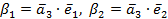 и вектор
и вектор 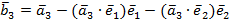 .
.
Нормируя вектор 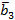 , получаем третий вектор ортонормированного базиса
, получаем третий вектор ортонормированного базиса 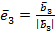 .
.
Продолжая процесс ортогонализации, по заданному базису 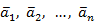 построим ортонормированный
построим ортонормированный 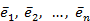 .
.
Упражнение. Проверить, что векторы 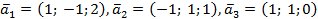 образуют ортогональный базис пространства
образуют ортогональный базис пространства 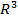 . Найти координаты вектора
. Найти координаты вектора 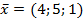 в этом базисе.
в этом базисе.
Определение 18. Направляющие косинусы вектора 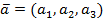 - это косинусы углов между вектором и осями координат. Вычисляют по формулам:
- это косинусы углов между вектором и осями координат. Вычисляют по формулам:
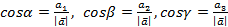 .
.
Таким образом, направляющие косинусы являются координатами нормированного вектора 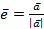 и
и
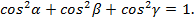
Примером базиса в Rп может служить лестничная система векторов
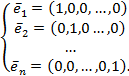
Если вектор 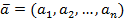 произвольный вектор из Rп, то очевидное равенство
произвольный вектор из Rп, то очевидное равенство
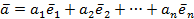
показывает, что 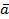 есть линейная комбинация векторов
есть линейная комбинация векторов 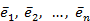 .
.
Пример.Одним из способов определения индекса цен и уровня инфляции является расчёт стоимости «потребительской корзины», состоящей из 300 видов товаров и услуг, получаемых городскими (или сельскими) потребителями. Ниже следующей таблицы приведён условный пример того, как можно вычислять индекс цен для определённого месяца по отношению к предыдущему месяцу.
Таблица 1
| Вид товара | Количество | Цена ед. товара в текущем месяце | Расходы в текущем месяце | Цена ед. товара в предыдущем месяце | Расходы в предыдущем месяце |
| Яйца Хлеб Кассеты | |||||
| Общие расходы | - | - | - |
Расчёт индекса цен: 40000/37500·100%=106,7%. Таким образом, индекс инфляции составил 6,7%.
Обозначим через 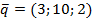 - вектор количества потребляемых товаров,
- вектор количества потребляемых товаров, 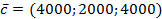 – вектор цен в текущем месяце,
– вектор цен в текущем месяце, 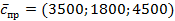 - вектор цен в предыдущем месяце. Тогда индекс цен вычисляется по формуле
- вектор цен в предыдущем месяце. Тогда индекс цен вычисляется по формуле
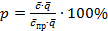 ,
,
откуда 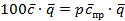 или
или 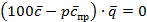 .
.
Таким образом, индекс цен можно определить как численный коэффициент р, который делает вектор 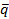 ортогональным вектору
ортогональным вектору 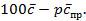
Индекс инфляции рассчитывается по формуле
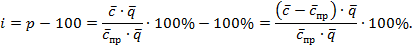
Практика
1. Векторы. Кремер. №3.24, 3.25, 3.28,3.34, 3.39….
2. Векторные пространства. №3.59, 3.60,3.68, 3.85
Домашнее задание
№3.29, 3.32, 3.35, 3.38, 3.74-3.76,386
Дата добавления: 2016-10-17; просмотров: 1739;
