Определители и их свойства
Непосредственное вычисление определителей второго и третьего порядка. Формула разложения определителя по строкам и столбцам.
Каждой квадратной матрице 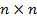 по некоторому закону может быть поставлено в соотвествие число
по некоторому закону может быть поставлено в соотвествие число 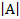 , называемое определителем матрицы А или просто определителем п-го порядка. Обозначают:
, называемое определителем матрицы А или просто определителем п-го порядка. Обозначают: 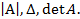
1) Определителем матицы 1-го порядка 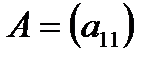 , называется элемент
, называется элемент 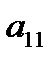 .
.
2) Определителем матрицы 2-го порядка называется число, вычисляемое по формуле:
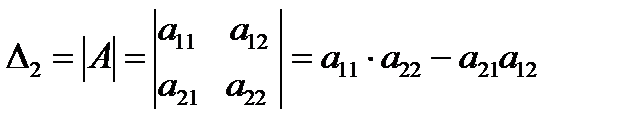 .
.
Пример 1.5. Вычислить определитель матрицы 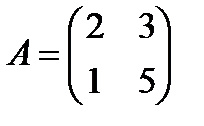 .
.
Решение. 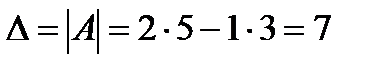 .
.
3) Определителем матрицы 3-го порядка называется число, вычисляемое по формуле:
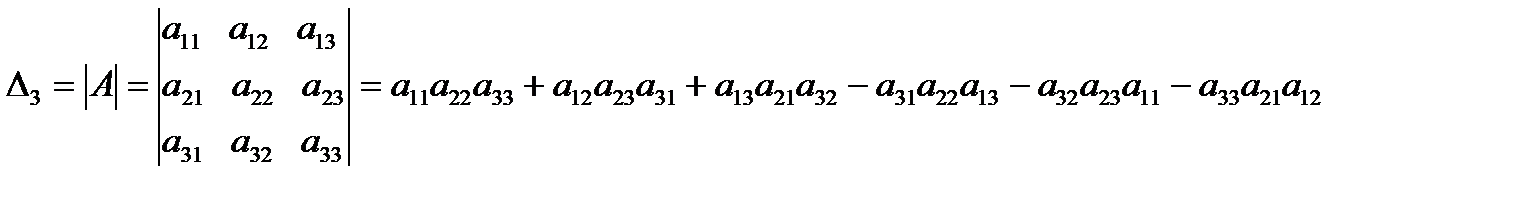
Данная формула получила название правила треугольников.

Пример 1.6. Вычислить определитель 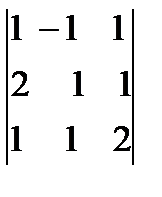 .
.
Решение. 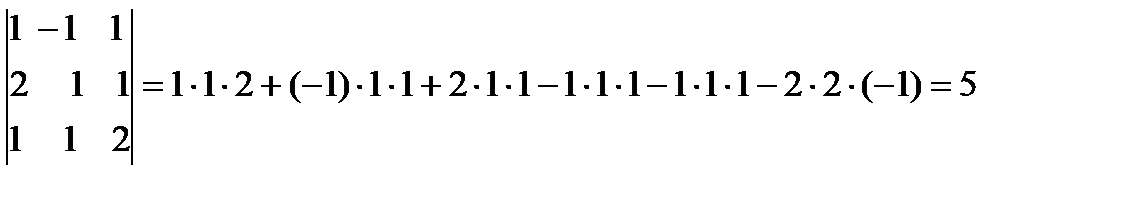 .
.
4) Определитель квадратной матрицы 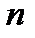 -го порядка (определитель
-го порядка (определитель 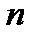 -го порядка).
-го порядка).
Определение. Минором 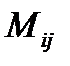 элемента
элемента 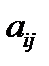 матрицы
матрицы 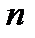 -го порядка называется определитель матрицы
-го порядка называется определитель матрицы 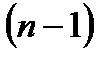 -го порядка, полученной из матрицы
-го порядка, полученной из матрицы 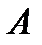 вычеркиванием
вычеркиванием 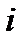 -й строки и
-й строки и 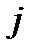 -го столбца.
-го столбца.
Определение. Алгебраическим дополнением 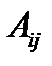 элемента
элемента 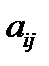 матрицы
матрицы 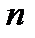 -го порядка называется минор, взятый со знаком
-го порядка называется минор, взятый со знаком 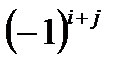 :
:
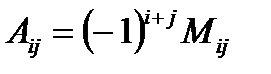 .
.
Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:
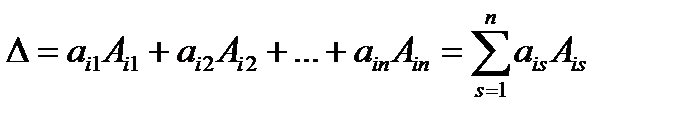
(разложение по элементам 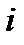 -й строки;
-й строки; 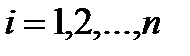 ).
).
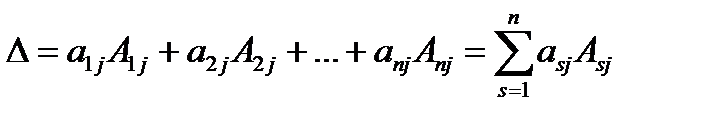
(разложение по элементам 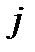 -го столбца;
-го столбца; 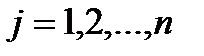 ).
).
Дата добавления: 2016-10-17; просмотров: 748;
