Аксиомы (свойства). Числовые характеристики: предельные и средние продукты, эластичность выпуска по факторам

Аксиома1.При отсутствии хотя бы одного ресурса производство невозможно, т.е. выпуск отсутствует.

Зависимость выпуска продукции y от факторов производства x={x1, …, xn} выражает формула y=f(x). В случае, если x_i = 0 хотя бы для одного i = 1, 2, ..., n, то согласно сформулированной аксиоме получаем выпуск y = 0.

Соответствие этому требованию означает, что математический вид формулы у=f(x) не может иметь свободного члена (не зависящего от x₁, x₂,…, x_i,… ,x_n). Наличие свободного члена означало бы, что выпуск возможен при нулевых значениях всех факторов.

Аксиома 2.Увеличение количества любого ресурса не может приводить к снижению объема выпуска продукции. Иначе говоря, выпуск продукции при дополнительном использовании малой единицы i-го ресурса производства не может быть меньше нуля.

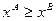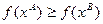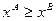Неравенство влечет , где означает 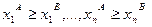. Это условие неубывания функции f по всем аргументам. Его можно проверить с помощью производных. Пусть существуют

.

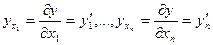Показатели 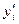- предельные продукты предприятия или предельные эффективности факторов. Приближенно можно считать при 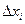=1, что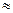 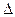y_i y_i.

Аксиома 3.Увеличение масштаба производства происходит с некоторой степенью однородности.

Математически степень однородности определяется следующим образом. Если зависимость выпуска продукции от факторов производства формализовать в виде y = f(x), x={x₁, … ,x_n}, i = 1, ... ,n, то рост масштаба производства означает пропорциональное увеличение значения всех факторов в λ (λ > 1) раз, факторы становятся равными λx. При этом выпуск продукции увеличится до y_λ. Формулу выпуска продукции после увеличения масштаба производства можно записать в следующем виде:

,

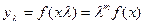где т – показатель степени однородности.

Следовательно, степень однородности производственной функции отражает эффект от изменения масштаба производства. Одинаковое увеличение масштаба разных производств может давать не одинаковый прирост выпуска продукции. Иначе говоря, рост масштаба производства может происходить с различной эффективностью. Отдача ресурсов при увеличении масштаба производства у одних предприятий может увеличиваться, у других – сокращаться, у третьих – оставаться без изменения.

Если показатель степени однородности m >1, то увеличение масштаба производства обеспечивает рост эффективности ресурсов. Если 0 < m < 1, то увеличение масштаба производства продукции уменьшает эффективность ресурсов. В случае m = 1 эффективность ресурсов не меняется, т. е. при увеличении масштаба производства происходит без изменения производительности ресурсов. Итак, если m = 1, то при увеличении значений факторов в λ раз выпуск продукции достигнет

y_λ = f(λ x) = λ f(x) = λ y.

Значит, эффективность применения ресурсов не изменится.

Чем существеннее увеличение производительности дополнительно вводимых ресурсов, тем выше значение показателя степени однородности. Если m >1, то при увеличении значения всех факторов в λ раз объем производства возрастет больше чем в λ раз.

Аксиома 4.График поверхности производственной функции является выпуклым вверх.

При росте выпуска продукции может происходить не только увеличение количества используемых ресурсов, но и изменение их структуры, т. е. один вид ресурса может частично замещаться другими видами. Например, при замене станков более производительными стоимость оборудования может увеличиться в большей мере, чем численность рабочих. Иными словами, при совокупном приросте использования ресурсов живой труд можно наращивать меньше, чем капитал.

По любым трем точкам x^A, x^B и x^C в многомерном пространстве факторов производства выпуклость вверх определяется неравенством

f(x^C) ≥ α f(x^A) + β f(x^B),

где x^C = α x^A + β x^B при любых 0 ≤ α, β ≤ 1, α + β = 1; x^A ≥ 0, x^B ≥ 0 и x^A ≠ x^B.

Неравенство x^A ≥ x^B означает 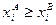для всех i = 1, … ,n.

Для иллюстрации замещения ресурсов при изменении выпуска продукции на рис. 3.1 показаны линии пересечения поверхности горизонтальными плоскостями на уровне объема выпуска y^А и y^B. Любая точка кривой 1 соответствует набору ресурсов для выпуска продукции y^А, а кривой 2 – набору для выпуска y^B. Применение ресурсов в количестве 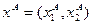обеспечивает выпуск y^А, увеличение ресурса x₂ с 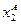до 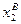и уменьшение ресурса 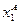до 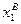дает прирост выпуска продукции с y^А до y^B. На рис. 3.1 этот переход обозначен жирной стрелкой.

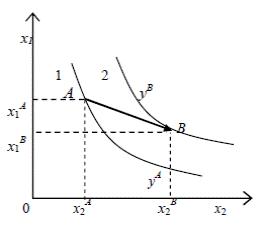
Рис. 3.1.

Пусть функция y(x) имеет второй дифференциал (например, существуют вторые частные производные и они непрерывны). Из этих производных составляется симметричная матрица Гессе:

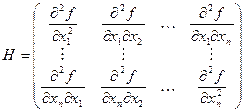
Выпуклость вверх означает отрицательную полуопределенность матрицы Н, что эквивалентно условию (Нх, х) 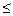0 для любого .

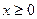Для выпуклости вверх поверхности ПФ в области определения необходимо и достаточно, чтобы главные нечетные миноры, начиная с первого порядка, матрицы H были не больше нуля, а главные четные миноры, начиная со второго порядка, были не меньше нуля.

Производительность ресурсов оценивается при помощи показателей отдачи. В микроэкономике понятие отдачи ресурсов специфично. В этом понятии с одной стороны выступает выпуск продукции (или его денежное выражение: доход, объем реализации), с другой – количество используемых ресурсов (или оплата их приобретения) за некоторый период времени. Показатели отдачи ресурсов выражают экономическую эффективность от их введения в производство. Они конкретизируют общее представление о соответствующих показателях.

Широко применяют показатели отдачи ресурсов трех типов:

• средняя отдача ресурсов производства,

• предельная отдача ресурсов производства,

• эластичность выпуска по ресурсам производства.

Все показатели производительности факторов вычисляют при изменении только одного ресурса.

Введем математические формулы этих показателей и рассмотрим их вычисление в случае двухфакторной производственной функции, отражающей зависимость выпуска продукции от вектора используемых ресурсов.

Средний продукт(средняя отдача) ресурса вычисляется делением объема выпуска на величину использования каждого ресурса. В случае двухфакторной ПФ применяют следующие формулы:

• средний продукт капитала – ,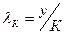

• средний продукт труда – .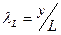

Поясним смысл показателя среднего продукта капитала с помощью графика зависимости выпуска продукции y от использования капитала K при постоянном значении L (рис. 3.2).

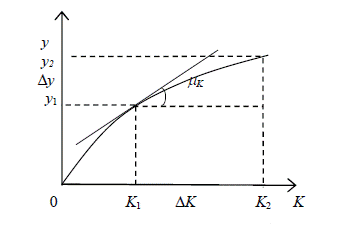
Рис 3.2.

При выпуске y₁ используют капитал в количестве K₁, средний продукт равен y₁/K₁. При выпуске y₂ используемый капитал составляет K₂, а средний продукт капитала – y₂/K₂. Выпуск продукции и используемый капитал относятся к числу интервальных показателей.

Графически этот показатель равен тангенсу угла наклона луча, проходящего через начало координат и точки определения показателя (K₁, y₁) или (K₂, y₂) и т.д. Период времени, в течение которого выпускают продукцию и используют ресурсы, один и тот же.

Итак, средний продукт капитала определяет объем выпуска продукции на каждую единицу используемого капитала за некоторый период времени.

Аналогичным образом вводится показатель среднего продукта труда, который выражает объем выпуска продукции на каждую единицу используемого труда.

Таким образом, средняя отдача (средний продукт) ресурса – это количество выпускаемой продукции на единицу соответствующего ресурса, используемого в производстве.

Используя математическую формулу ПФ Кобба – Дугласа, эти показатели можно вычислить аналитически. Средняя отдача ресурсов определяется по следующим формулам.

Средний продукт капитала – по формуле:

,

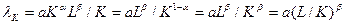учитывая, что 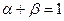для ПФКД.

Если обозначить отношение используемого капитала к трудозатратам буквой 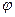, то получим формулу: .

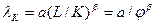Средний продукт труда имеет вид:

.

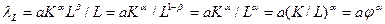Предельный продукт(предельная отдача) ресурса вычисляется по формуле частной производной производственной функции по фактору производства. Для двухфакторной ПФ применяют следующие формулы:

• предельный продукт капитала – ,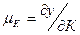

• предельный продукт труда – .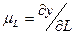

Графически предельный продукт капитала равен тангенсу угла наклона касательной к линии выпуска в точке определения показателя(см. рис. 3.2).

Если зависимость выпуска от фактора задана дискретно и прирост выпуска 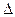y требует дополнительного использования капитала в количестве 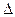K, то предельную отдачу вычисляют по формуле μ_K = 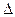y/ 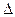K. Пределом этого отношения при 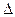K → 0 является выражение 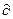y/ 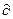K. Аналогично вычисляется предельный продукт труда.

Таким образом, предельный отдача ресурса выражает прирост выпускаемой продукции на единицу прироста соответствующего ресурса, используемого в производстве.

Применительно к ПФ Кобба – Дугласа можно вывести следующие формулы предельной отдачи ресурсов:

предельный продукт капитала –

;

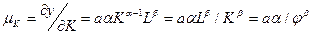предельный продукт труда –

.

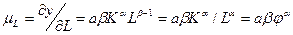Рассмотрим соотношение средней отдачи капитала 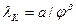и предельной отдачи капитала 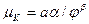. Из этих формул следует, что 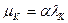. Вместе с тем 0 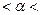1, следовательно, μ_K < λ_K. Аналогично из уравнени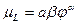й и 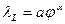следует, что 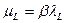. Учитывая, что 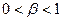, получаем неравенство 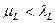. Иначе говоря, в модели Кобба – Дугласа предельные продукты капитала и труда имеют меньшие значения, чем средние продукты этих ресурсов производства.

Теорема Эйлера.Рассматривается некоторая непрерывно дифференцируемая функция y = f(x), причем f(x) – однородная функция степени m ( 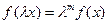). Тогда справедливо равенство:

.

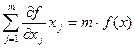Из этой теоремы следует, что предельная производительность от масштабов производства:

.

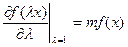Тогда по теореме Эйлера эластичность выпуска от масштабов производства есть отношение предельной производительности к средней величине :

,

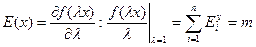где 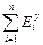- сумма эластичностей по факторам.

Таким образом, эластичность от масштаба производства Е(x) для производственной функции степени однородности m в точности равна m.

Предельная норма замещения (замены) i-го ресурса j-го ресурсом показывает сколько единиц j-го ресурса высвобождается при увеличении i-го ресурса на одну бесконечно малую единицу (иногда встречается термин «предельная технологическая норма замещения»).

Пусть дана производственная функция 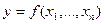. Предельная норма замещения определяется выражением 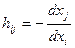. Зафиксируем выпуск у= 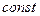и будем изменять 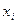и 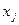. Имеем:

,

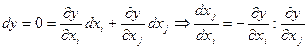следовательно, .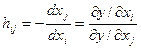

Для ПФ Кобба-Дугласа 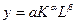находим 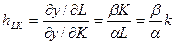, где 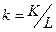- фондовооруженность.

Эластичность замены (замещения)показывает на сколько процентов изменится отношение факторов при изменении предельной нормы замещения на бесконечно малый процент:

.

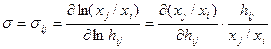Эластичность замены  это мера кривизны изоквант; линий уровня; производственных линий безразличия (в общем случае, поверхностей уровня, поверхностей безразличия).

Эластичность замещения показывает, на сколько процентов изменится тангенс угла наклона изоклинали при изменении тангенса угла наклона касательной к изокванте на один процент. Величина 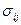ij означает некоторую инвариантную величину. Для ПФ Кобба-Дугласа 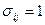, т.к. вхождение труда и капитала в данной модели одинаково.

Теорема.Для однородной производственной функции предельная замещения труда капиталом h_LK зависит лишь от фондовооруженности 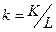и остается постоянной вдоль лучей, выходящих из нулевой точки.