I. Аксиомы принадлежности
Схема построения геометрии
Перечисляются основные неопределяемые понятия.
Формулируются свойства основных понятий - аксиомы.
Определяются другие геометрические понятия.
Формулируются и доказываются свойства геометрических понятий - теоремы.
АКСИОМЫ СТЕРЕОМЕТРИИ. СЛЕДСТВИЯ ИЗ АКСИОМ
Основные понятия стереометрии: точка, прямая, плоскость, расстояние.
Определение: Аксиомой называется предложение, не требующее доказательства.
Основные свойства точек, прямых и плоскостей, касающиеся их взаимного расположения, выражены в аксиомах. Вся система аксиом стереометрии состоит из ряда аксиом, известных нам по курсу планиметрии, и аксиом о взаимном расположении точек, прямых и плоскостей в пространстве.
АКСИОМЫ СТЕРЕОМЕТРИИ
I. Аксиомы принадлежности
I1. Существуют хотя бы одна прямая и хотя бы одна плоскость. Каждая прямая и каждая плоскость есть не совпадающее с пространством непустое множество точек.
Обозначение:
А, В, С, D – точки;
а, b, с – прямые;
a , b , g – плоскости;
А Î а – точка А принадлежит прямой а, прямая а проходит через точку А;
Е Ï а – точка Е не принадлежит прямой а;
С Î a – точка С принадлежит плоскости a , плоскость a проходит через точку С;
Е Ï a – точка Е не принадлежит плоскости a .
Вывод: Существуют точки, принадлежащие прямой и не принадлежащие прямой, существуют точки, принадлежащие плоскости и не принадлежащие плоскости.
I2. Через две различные точки проходит одна и только одна прямая.
 |
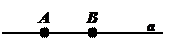Обозначение: а = АВ
Вывод: Прямые, имеющие две различные общие точки, совпадают.
I3. Прямая, проходящая через две любые точки плоскости, лежит в этой плоскости.
 |
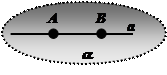Обозначение:
а Ì a – плоскость a проходит через прямую а;
b Ë a – плоскость a не проходит через прямую b.
I4. Через три точки, не принадлежащие одной прямой, проходит одна и только одна плоскость.
Обозначение: a = АВС
Вывод: Плоскости, имеющие три различные общие точки, совпадают.
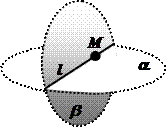
I5. Если две различные плоскости имеют общую точку, то их пересечением является прямая.
Обозначение: М Î a , М Î b , a ¹ b , a ìüb = l.
Дата добавления: 2016-05-11; просмотров: 3542;