Аксиомы аддитивности
3.1. 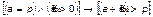 .
.
3.2. 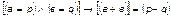 .
.
3.3. 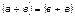 (свойство симметричности).
(свойство симметричности).
3.4. 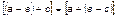 (свойство ассоциативности).
(свойство ассоциативности).
Если выполняются аксиомы только первой группы, то соответствующая шкала называется шкалой наименований. В пределах шкалы данного типа оценка ценности структурных образований невозможна. Это шкала их ситуационного различения. Типичным примером здесь может служить перечень инвентарных номеров документов. Заметим, что не все отношения, существующие в эмпирических системах, удовлетворяют даже этой простейшей системе аксиом. Так, например, из условия, что А есть друг В и В есть друг С, не всегда следует, что А есть друг С. Это означает нетранзитивность отношения дружественности в группе аксиом тождества. Поэтому не всегда бывает возможным составить вполне однозначный и непротиворечивый список друзей некоторой компании.
Если для отношения, существующего между элементами эмпирической системы, выполняются аксиомы первой и второй групп, то мы имеем дело с различными шкалами порядка (строгого или слабого, полного или частичного) в зависимости от того, какие аксиомы второй группы выполняются для тех или иных подмножеств шкалы. Шкалы порядка дают возможность качественной оценки ценности. Например, в шкале порядка измеряются приоритеты распределения ресурсов среды таких качественно различных отраслей, как промышленность, наука, здравоохранение, культура и т.п. В шкале порядка измеряются также предпочтительность различных видов товаров и услуг. Необходимо заметить, аксиомы порядка для некоторых отношений также не всегда являются справедливыми.
И, наконец, если для эмпирической системы Sе выполняются все три группы аксиом, то соответствующая шкала называется шкалой интервалов. Для шкалы интервалов допустимым преобразованием, совершаемым на числовом множестве Sn, является линейное преобразование вида:
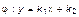 ,
, 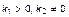 , (1.3.5)
, (1.3.5)
где x и y – числовые переменные, характеризующие отношения между элементами Sе в Sn, k1 – масштаб измерения, k2 – начало отсчета.
Типичным примером шкалы интервалов является шкала температур. Казалось бы, для Sе, удовлетворяющей шкале отношений, аксиомы 3.1 и 3.4 не выполняются, так что в этой шкале операция сложения не является законной. Однако система отношений в Sn допускает свое доопределение, т.е. для нее становятся выполненными аксиомы аддитивности, что позволяет перейти к шкале отношений.
Если k2 = 0, то шкала интервалов превращается в шкалу отношений. В шкале отношений измеряются, например, такие характеристики структурных образований, как масса, длина, объем, энергия, цена, время и т.п.
Шкала интервалов может быть легко преобразована в шкалу отношений. Для этого необходимо перейти к новой переменной z:
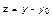 , (1.3.6)
, (1.3.6)
где
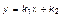 ,
,
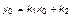 ,
,
x0 – значение переменной y, соответствующее некоторому конкретному значению переменной x.
 Числовое утверждение в Sn шкалы Ш является адекватным ситуации в Sn, если его истинность не меняется при любом допустимом для шкалы преобразовании j.
Числовое утверждение в Sn шкалы Ш является адекватным ситуации в Sn, если его истинность не меняется при любом допустимом для шкалы преобразовании j.
Особенно часто вопрос об адекватности возникает при попытке получения общего интегративного мнения на основе некоторой совокупности не вполне совпадающих оценок какой-либо вещи, события или явления. Ведь для получения результирующего утверждения исходные суждения должны быть подвергнуты некоторой математической операции объединения (например, усреднения индивидуальных суждений). И если это преобразование является недопустимым в данной шкале, то результирующее утверждение может оказаться неадекватным. Физически допустимое преобразование, например, реализуется при замене одного эксперта другим, имеющим точно такие же порядковые предпочтения, но выставляющим другие более сглаженные или, наоборот, более резко отличающиеся количественные оценки.
Пусть отношение между элементами эмпирической системы Sе удовлетворяет аксиомам только первой и второй групп. И пусть для этой системы справедливо утверждение
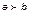 , (1.3.7)
, (1.3.7)
где 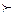 – символ, обозначающий отношение предпочтительности. Очевидно, оно будет эквивалентно утверждению на числовом множестве Sn
– символ, обозначающий отношение предпочтительности. Очевидно, оно будет эквивалентно утверждению на числовом множестве Sn
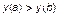 (1.3.8)
(1.3.8)
(где 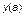 и
и 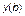 – числа), если соответствующая шкала является шкалой порядка и
– числа), если соответствующая шкала является шкалой порядка и
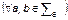
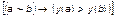 . (1.3.9)
. (1.3.9)
Однако если на числовом множестве мы зададим утверждение
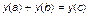 , (1.3.10)
, (1.3.10)
то оно, очевидно, будет неадекватным, так как допустимое для шкалы преобразование 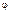 (например, возведение в квадрат) может нарушить справедливость этого утверждения
(например, возведение в квадрат) может нарушить справедливость этого утверждения
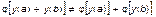 . (1.3.11)
. (1.3.11)
Условие адекватности довольно часто нарушается при обработке числовой информации, связанной с различного рода опросами и экспертизами. Для суждений, высказываемых экспертами, уровень измеримости, как правило, соответствует шкале порядка, а иногда и просто шкале наименований, и поэтому такие операции, например, как определение среднего или среднеквадратичного отклонения являются незаконными, поскольку могут привести к нарушению адекватности числовых утверждений реальной ситуации. При измерениях в порядковых шкалах в качестве аналога среднего рекомендуется использовать медиану вариационного ряда
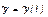 , (1.3.12)
, (1.3.12)
где l ‑ целая часть величины 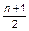 ,
, 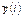 – вариационный ряд переменной y, записанный и пронумерованный в порядке возрастания ее величины;
– вариационный ряд переменной y, записанный и пронумерованный в порядке возрастания ее величины; 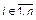 .
.
Действительно, отношения порядка в пределах вариационного ряда
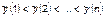 (1.3.13)
(1.3.13)
не изменятся при использовании допустимого для порядковой шкалы преобразования 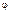 :
:
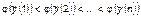 , (1.3.14)
, (1.3.14)
т.е. положение медианы при таком преобразовании не изменяется. Если же мы воспользуемся недопустимым в данном случае преобразованием
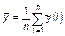 , (1.3.15)
, (1.3.15)
то при применении к данному утверждению другого допустимого преобразования произошло бы нарушение его истинности
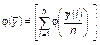 . (1.3.16)
. (1.3.16)
Таким образом, оценка среднего в порядковой шкале может оказаться неадекватной реальной ситуации.
Заметим, что номер оценки вариантного ряда, фиксируемый для выбора, может быть в принципе любым, – все равно получаемое в результате этого выбора утверждение будет адекватным в смысле приведенной выше формулировки. Однако медианное оценивание является наиболее взвешенным, учитывающим весь разброс суждений относительно каждого оцениваемого признака, а не только крайние или близкие к ним суждения. В этом смысле медианная оценка – срединная, а не крайняя. При медианном оценивании важен порядок (профиль) предпочтений, а не их количественные оценки. С практической точки зрения устойчивость утверждений в Sn относительно допустимых преобразований может рассматриваться, например, как устойчивость общего мнения на множестве эквивалентных в смысле порядка индивидуальных предпочтений групп экспертов. При этом суждения двух экспертов считаются эквивалентными, несмотря на различия их количественных оценок, если порядок их предпочтений на множестве оцениваемых признаков совпадает (табл. 1.3.1).
Таблица 1.3.1
| Мнение экспертов | Объект оценивания | |||
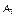
| 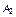
| 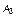
| 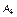
| |
| 4,1 | 4,3 | 4,2 |
При этом две группы экспертов считаются эквивалентными, если между ними существует бинарное отношение взаимно однозначного соответствия суждений, составляющих их экспертов. Таким образом, число в порядковых шкалах имеет символический, качественный, а не количественный смысл.
 Символический характер числовых оценок в порядковых шкалах проиллюстрируем на следующем примере. Пусть три эксперта некоторой фирмы, рассмотрев шесть возможных инвестиционных проектов, выставили следующие балльные оценки (по десятибалльной шкале) (табл. 1.3.2).
Символический характер числовых оценок в порядковых шкалах проиллюстрируем на следующем примере. Пусть три эксперта некоторой фирмы, рассмотрев шесть возможных инвестиционных проектов, выставили следующие балльные оценки (по десятибалльной шкале) (табл. 1.3.2).
Таблица 1.3.2
Таблица оценок инвестиционных проектов
| Эксперт | Проект | |||||
| Суммарный балл | ||||||
| Медиана |
По сумме баллов наиболее предпочтительным является шестой проект инвестирования, а согласно медианному оцениванию – пятый. После некоторого размышления эксперты изменили свои мнения и выставили следующие оценки рассматриваемым проектам (табл. 1.3.3).
Как видно из табл. 1.3.3, победитель по сумме баллов изменился. Им стал пятый проект. Но если мы сравним индивидуальные профили предпочтений в обеих таблицах, то легко обнаружим, что они в шкале порядка не изменились – изменились лишь числовые символы этих предпочтений. Но поскольку в данном случае речь идет о качественном оценивании, то результирующее коллективное мнение не должно зависеть от того, какими символами обозначат свои предпочтения эксперты. Ведь в порядковой шкале две записи, выражающие предпочтение первым экспертом шестого проекта относительно пятого,
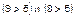
качественно не изменились.
Таблица 1.3.3
Уточнение инвестиционных проектов
| Эксперт | Проект | |||||
| Суммарный балл | ||||||
| Медиана |
Заметим, что в приведенном примере наилучший проект, выбираемый на основе медианной оценки, остался прежним (это пятый проект).
Дата добавления: 2016-12-08; просмотров: 1498;
