Элементы формальной ценностной теории голосований
 Ценностная окраска ситуационных образов, возникающих в сознании членов человеческого сообщества, является основным движущим стимулом, формирующим их предпочтения на множестве предложенных для выбора альтернатив. На рис. 1.3.3 представлена схема взаимосвязи структурных компонент существующего и желаемого состояний системы ценностей индивида, принадлежащего некоторой социальной группе, со структурными компонентами ситуаций, которые существуют или могут существовать в различных сферах внешнего мира.
Ценностная окраска ситуационных образов, возникающих в сознании членов человеческого сообщества, является основным движущим стимулом, формирующим их предпочтения на множестве предложенных для выбора альтернатив. На рис. 1.3.3 представлена схема взаимосвязи структурных компонент существующего и желаемого состояний системы ценностей индивида, принадлежащего некоторой социальной группе, со структурными компонентами ситуаций, которые существуют или могут существовать в различных сферах внешнего мира.
Системы ценностей (системы ценностных предпочтений) индивидов, принадлежащих разным социальным группам, довольно существенно отличаются друг от друга (рис. 1.3.4). Очевидно, что ситуации, возникающие в рассматриваемых сферах, самым непосредственным образом влияют (и это, если и не понимает вполне отчетливо, то по крайней мере чувствует каждый индивид) на степень удовлетворения его интересов и потребностей. Вследствие этого ситуации в сферах внешнего мира приобретают для индивида соответствующую ценностную окраску. Характер и степень проявления взаимосвязи сфер и системы ценностей зависят от индивидуальных свойств человека, его социального положения и от той роли, которую он играет в жизни общества.
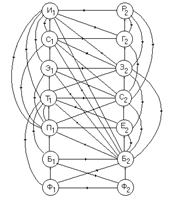
| Рис. 1.3.3. Схема взаимосвязей (взаимодействия) структурных компонент внешнего мира и системы ценностей индивида: Ф1, Б1, П1, Т1, Э1, С1 и И1 – физическая, биологическая, психологическая, технологическая, экономическая, социально-политическая и информационные сферы соответственно; Ф2, Б2, П1, Е2, С2, З2, Г2, Р2 – ценностные потребности индивида: физиологические (материальные), в защищенности, в единении с другими членами общества, в самоутверждении, в знаниях, в гармонии (этические и эстетические) и в саморазвитии |
Таким образом, принятие того или иного решения в процессе голосования конкретным гражданином, его выбор определяется в первую очередь ситуациями, которые могут возникнуть по представлениям этого гражданина в его системе ценностей (точнее, в ценностном образе внешнего мира) при избрании того или иного кандидата. При этом он, разумеется, базируется на своем модельном представлении (чаще всего чисто интуитивном) о взаимосвязи состояний сфер и системы ценностей. И в этом смысле избиратель отдает свое предпочтение тому кандидату, образ которого наиболее близок к его идеалу.
Формально ситуацию в сферах, существующую на некотором временном интервале Т, можно охарактеризовать множеством значений векторной функции 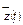 , заданных на этом интервале. И в этом смысле соответствующее этой ситуации состояние системы ценностей индивида, принадлежащего социальной группе i, представляет собой отображение
, заданных на этом интервале. И в этом смысле соответствующее этой ситуации состояние системы ценностей индивида, принадлежащего социальной группе i, представляет собой отображение
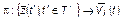 ,
,
где 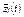 – вектор переменных состояния системы ценностей; t – момент времени.
– вектор переменных состояния системы ценностей; t – момент времени.
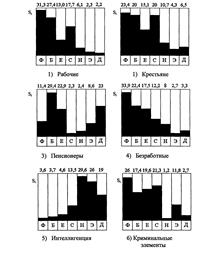
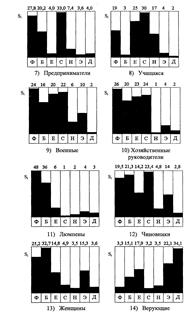
Рис. 1.3.4. Системы ценностей некоторых социальных групп
Нижегородской области, реконструированные на основе обработки
результатов опроса с помощью метода анализа иерархий
(обозначения те же, что и на рис. 1.3.3)
Очевидно, что ситуация в сферах складывается под влиянием некоторой совокупности факторов 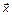 , действующих в указанных сферах в течение интервала времени
, действующих в указанных сферах в течение интервала времени 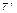 , который, вообще говоря, не совпадает с
, который, вообще говоря, не совпадает с 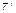 , т.е. существует отображение
, т.е. существует отображение 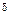 :
:
 .
.
Отсюда следует, что ценностно окрашенные модельные ценностные представления о внешнем мире любого индивида формально могут быть выражены с помощью отображения
 .
.
Таким образом, каждый фактор х (переменный или постоянный), характеризующийся совокупностью своих значений на интервале 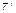 и ценностно различимый индивидом, приобретает в глазах последнего соответствующую ценностную окраску, которая формально может быть выражена в виде некоторой спектральной функции
и ценностно различимый индивидом, приобретает в глазах последнего соответствующую ценностную окраску, которая формально может быть выражена в виде некоторой спектральной функции 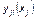 . Опираясь именно на это представление (достаточно полное или частичное) о ценности существующих и желаемых ситуаций в сферах, и совершает свой выбор данный индивид. Хотя система ценностей социальной группы и несколько размыта (расплывчата), тем не менее она достаточно типична для представителей этой группы, что делает их выбор в значительной степени согласованным и предсказуемым.
. Опираясь именно на это представление (достаточно полное или частичное) о ценности существующих и желаемых ситуаций в сферах, и совершает свой выбор данный индивид. Хотя система ценностей социальной группы и несколько размыта (расплывчата), тем не менее она достаточно типична для представителей этой группы, что делает их выбор в значительной степени согласованным и предсказуемым.
 Среднее относительное число голосов, которое может быть отдано за кандидата (альтернативу) k, следующим образом зависит от статистических характеристик избирательной системы:
Среднее относительное число голосов, которое может быть отдано за кандидата (альтернативу) k, следующим образом зависит от статистических характеристик избирательной системы:
 , (1.3.58)
, (1.3.58)
где nk – общее число голосов, которые могут быть отданы в среднем за кандидата (альтернативу) k; n – количество различных социальных групп населения в рассматриваемом округе, существенно отличающихся друг от друга своими системами ценностей; Pi – доля избирателей данного округа; 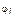 – доля избирателей в группе i, которые примут участие в голосовании;
– доля избирателей в группе i, которые примут участие в голосовании; 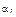 – доля избирателей в группе i от числа голосующих, которые сделают свой выбор случайно; Pki –средняя доля избирателей от числа делающих свой выбор не случайно, которые проголосуют за кандидата k.
– доля избирателей в группе i от числа голосующих, которые сделают свой выбор случайно; Pki –средняя доля избирателей от числа делающих свой выбор не случайно, которые проголосуют за кандидата k.
Вероятности Pki представляют собой некоторые функции кажущейся ценности  кандидата k для избирателей социальной группы i;
кандидата k для избирателей социальной группы i;
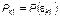 . (1.3.59)
. (1.3.59)
Очевидно, что чем выше  , тем ближе образ этого кандидата к идеалу. При формализации зависимости
, тем ближе образ этого кандидата к идеалу. При формализации зависимости 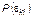 необходимо учитывать несколько обстоятельств: во-первых, представление избирателя о том, насколько понимает существенную и желаемую ситуации тот или иной кандидат (кажущаяся привлекательность его позиции); во-вторых, представление избирателя о способности этого кандидата сохранить или изменить ситуацию в нужном направлении (ощущение способностей и возможностей); в-третьих, ощущение избирателем психологической привлекательности образа кандидата (привлекательность); в-четвертых, наличие у избирателя личной материальной или иной заинтересованности в избрании конкретного индивида (стимуляции выбора); в-пятых, наличие у избирателя достаточной для принятия решения информации о кандидате (информированность, известность).
необходимо учитывать несколько обстоятельств: во-первых, представление избирателя о том, насколько понимает существенную и желаемую ситуации тот или иной кандидат (кажущаяся привлекательность его позиции); во-вторых, представление избирателя о способности этого кандидата сохранить или изменить ситуацию в нужном направлении (ощущение способностей и возможностей); в-третьих, ощущение избирателем психологической привлекательности образа кандидата (привлекательность); в-четвертых, наличие у избирателя личной материальной или иной заинтересованности в избрании конкретного индивида (стимуляции выбора); в-пятых, наличие у избирателя достаточной для принятия решения информации о кандидате (информированность, известность).
Близость кажущейся позиции кандидата k по признаку 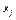 к идеальному для избирателей социальной группы i образу в случае непрерывности величины
к идеальному для избирателей социальной группы i образу в случае непрерывности величины 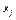 можно оценить с помощью выражения
можно оценить с помощью выражения
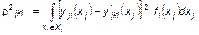 , (1.3.60)
, (1.3.60)
где 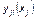 – спектральная функция, характеризующая степень проявления конкретного значения признака
– спектральная функция, характеризующая степень проявления конкретного значения признака 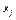 в идеальном для избирателей группы i образе;
в идеальном для избирателей группы i образе; 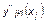 – соответствующая кажущаяся спектральная функция, характеризующая для избирателей группы i образ кандидата k;
– соответствующая кажущаяся спектральная функция, характеризующая для избирателей группы i образ кандидата k; 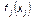 – ядро интегрального преобразования, характеризующее вес конкретного значения признака
– ядро интегрального преобразования, характеризующее вес конкретного значения признака 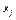 относительно всевозможных его значений.
относительно всевозможных его значений.
В случае, если признак 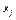 является дискретным, величина
является дискретным, величина 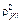 может быть представлена в виде
может быть представлена в виде

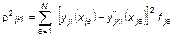 ,
,
где 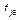 , в частности, может быть равна просто
, в частности, может быть равна просто 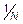 (N – общее число различных значений признака
(N – общее число различных значений признака 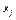 ;
; 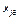 – e-е значение признака
– e-е значение признака 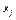 ).
).
В качестве признака 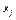 может, например, выступать социально-политическая ориентация. Характерными значениями этого признака являются: анархия, демократия, олигархия, диктатура и т.д.
может, например, выступать социально-политическая ориентация. Характерными значениями этого признака являются: анархия, демократия, олигархия, диктатура и т.д.
Значение  – означает положительное отношение избирателя (кандидата) к соответствующему значению признака
– означает положительное отношение избирателя (кандидата) к соответствующему значению признака 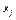 ;
; 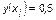 – нейтральное и
– нейтральное и 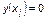 – отрицательное.
– отрицательное.
Спектральная функция 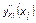 зависит от информации об образе кандидата k, имеющейся у избирателей, и от степени их доверия к его позиции. В связи с этим в линейном приближении можно записать
зависит от информации об образе кандидата k, имеющейся у избирателей, и от степени их доверия к его позиции. В связи с этим в линейном приближении можно записать
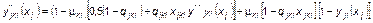 , (1.3.61)
, (1.3.61)
где 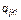 – степень известности кандидата k для избирателей социальной группы i (
– степень известности кандидата k для избирателей социальной группы i ( 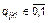 );
); 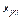 – степень доверия избирателей к кажущемуся образу кандидата k (
– степень доверия избирателей к кажущемуся образу кандидата k ( 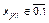 );
); 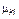 – доля скептически настроенных по отношению к кандидату k избирателей в группе i (
– доля скептически настроенных по отношению к кандидату k избирателей в группе i ( 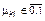 ).
).
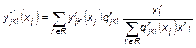 , (1.3.62)
, (1.3.62)
где 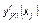 – спектральная функция образа кандидата k по признаку
– спектральная функция образа кандидата k по признаку 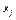 по сообщениям источника информации r;
по сообщениям источника информации r; 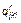 – степень известности избирателям группы i информации о степени и характере проявления признака
– степень известности избирателям группы i информации о степени и характере проявления признака 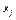 в образе кандидата k, приобретаемая по сообщениям источника информации r (
в образе кандидата k, приобретаемая по сообщениям источника информации r ( 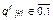 );
); 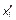 – степень доверия избирателей группы
– степень доверия избирателей группы 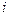 к источнику информации r (
к источнику информации r ( 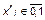 ).
).
Естественно считать, что
 .
.
Необходимо отметить, что во множество источников информации R входят и сами кандидаты, высказывающиеся не только о своих взглядах (позициях), но и о позициях других кандидатов.
Кажущаяся ценность кандидата k для избирателей социальной группы i является, очевидно, некоторой убывающей функцией вектора расстояний 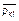 . Конкретный вид этой функции определяется типом системы ценностей. В связи с этим рассмотрим некоторые наиболее характерные из них.
. Конкретный вид этой функции определяется типом системы ценностей. В связи с этим рассмотрим некоторые наиболее характерные из них.
Дата добавления: 2016-12-08; просмотров: 671;
