СЛЕДСТВИЯ ИЗ АКСИОМ
Следствие 1: Через прямую и не принадлежащую ей точку можно провести одну и только одну плоскость.
 |
Дано: М, а, М Ï а
Доказать:
1. 
;
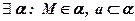2. 
.
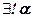Доказательство:
1. Выберем на прямой а точки А и В (аксиома I1): АÎ а, ВÎ а.
Через точки М, А, В проходит плоскость a (аксиома I4): a = МАВ.
Так как точки А, В принадлежат плоскости a , то прямая а принадлежит плоскости a (аксиома I3): а Ì a .
Следовательно, существует плоскость a , проходящая через прямую а и не принадлежащую ей точку М: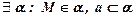 
.
2. Плоскость a содержит прямую а и точку М, то есть проходит через точки М, А, В. Через три точки, не принадлежащие одной прямой, проходит единственная плоскость (аксиома I4).
Следствие 2: Через две пересекающиеся прямые можно провести одну и только одну плоскость.
 |
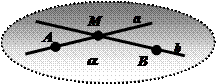Дано: а, b, а ´ b
Доказать:
1. 
;
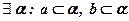2. .
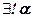Доказательство:
1. Обозначим точку пересечения прямых а и b: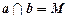 
.
Выберем на прямой а точку А, на прямой b точку В (аксиома I1): АÎ а, ВÎ b.
Через точки М, А, В проходит плоскость a (аксиома I4): a = МАВ.
Так как точки А, М принадлежат плоскости a , то прямая а принадлежит плоскости a (аксиома I3): АМ = а Ì a .
Так как точки В, М принадлежат плоскости a , то прямая b принадлежит плоскости a (аксиома I3): ВМ = b Ì a .
Следовательно, существует плоскость a , проходящая через две пересекающиеся прямые а и b: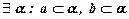 
.
2. Плоскость a содержит прямые а и b, то есть проходит через точки М, А, В. Через три точки, не принадлежащие одной прямой, проходит единственная плоскость (аксиома I4).
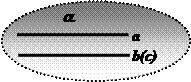Определение: Прямые называются параллельными, если они лежат в одной плоскости и не имеют общих точек или совпадают.
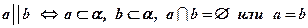
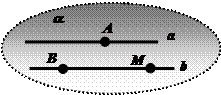Следствие 3: Через две параллельные прямые можно провести одну и только одну плоскость.
Дано: а, b,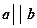 
Доказать:
1. ;
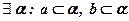2. .
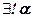Доказательство:
Дата добавления: 2016-05-11; просмотров: 1730;