Если плоскости a и b совпадают, то они параллельны по определению.
Пусть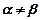 
.
Предположим, что плоскости a и b пересекаются: a ìüb = l.
Прямая а1 параллельна прямой а2 по условию, следовательно, по признаку параллельности прямой и плоскости прямая а1 параллельна плоскости b . А значит, по вспомогательной теореме, прямая а1 параллельна прямой l пересечения плоскостей a и b.
Прямая b1 параллельна прямой b2 по условию, следовательно, по признаку параллельности прямой и плоскости прямая b1 параллельна плоскости b . А значит, по вспомогательной теореме, прямая b1 параллельна прямой l пересечения плоскостей a и b.
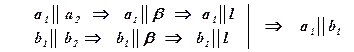
Если две прямые параллельны третьей прямой, то они параллельны, следовательно, прямые а и b параллельны. А это противоречит условию, так как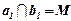 
. Следовательно, предположение не верно, а верно то, что требовалось доказать, то есть 
.
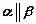Вывод: Чтобы доказать, что две данные плоскости параллельны, надо указать в первой плоскости две пересекающиеся прямые и во второй плоскости найти две прямые, каждая из которых параллельна одной из двух указанных прямых первой плоскости.
Упражнения:
1. Каким может быть взаимное расположение прямых а и b, каждая из которых лежит в одной из двух различных параллельных плоскостей?
Дата добавления: 2016-05-11; просмотров: 1008;