ТЕТРАЭДР. ПАРАЛЛЕЛЕПИПЕД
 В теме «Геометрические тела, их поверхности и объёмы» мы будем изучать многогранники – геометрические тела, поверхности которых составлены из многоугольников. Для иллюстрации понятий, связанных с взаимным расположением прямых и плоскостей в пространстве познакомимся с двумя многогранниками – тетраэдром и параллелепипедом.
В теме «Геометрические тела, их поверхности и объёмы» мы будем изучать многогранники – геометрические тела, поверхности которых составлены из многоугольников. Для иллюстрации понятий, связанных с взаимным расположением прямых и плоскостей в пространстве познакомимся с двумя многогранниками – тетраэдром и параллелепипедом.
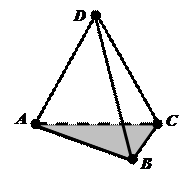
Рассмотрим произвольный треугольник АВС и точку D, не лежащую в плоскости этого треугольника. Соединив точку D отрезками с вершинами треугольника АВС, получим треугольники DАВ, DВС, DСА.
Поверхность, составленная из четырёх треугольников АВС, DАВ, DВС, DСА, называется тетраэдром и обозначается DАВС.
Треугольники, из которых состоит тетраэдр, называются гранями, их стороны – рёбрами, а вершины – вершинами тетраэдра. Тетраэдр имеет четыре грани, шесть рёбер и четыре вершины.
Два ребра тетраэдра, не имеющие общих вершин, называются противоположными. У тетраэдра DАВС противоположными являются рёбра АD и ВС, ВD и АС, СD и АВ. Часто одну из граней тетраэдра называют основанием, и три другие – боковыми гранями.
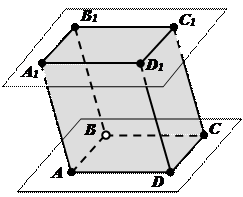 Рассмотрим два равных параллелограмма АВСD и А1В1С1D1, расположенных в параллельных плоскостях так, что отрезки АА1, ВВ1, СС1 и DD1 параллельны. Четырёхугольники АВВ1А1, ВСС1В1, СDD1С1, DАА1D1 также являются параллелограммами, так как каждый из них имеет попарно параллельные противоположные стороны.
Рассмотрим два равных параллелограмма АВСD и А1В1С1D1, расположенных в параллельных плоскостях так, что отрезки АА1, ВВ1, СС1 и DD1 параллельны. Четырёхугольники АВВ1А1, ВСС1В1, СDD1С1, DАА1D1 также являются параллелограммами, так как каждый из них имеет попарно параллельные противоположные стороны.
Поверхность, составленная из двух равных параллелограммов АВСD и А1В1С1D1 и четырёх параллелограммов АВВ1А1, ВСС1В1, СDD1С1, DА А1D1, называется параллелепипедом и обозначается АВСDА1В1С1D1.
Параллелограммы, из которых составлен параллелепипед, называются гранями, их стороны – рёбрами, а вершины параллелограммов – вершинами параллелепипеда. Параллелепипед имеет шесть граней, двенадцать рёбер и восемь вершин. Две грани параллелепипеда, имеющие общее ребро, называются смежными, а не имеющие общих рёбер – противоположными. Две вершины, не принадлежащие одной грани, называются противоположными. Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда. Каждый параллелепипед имеет четыре диагонали.
Диагоналями параллелепипеда АВСDА1В1С1D1 являются отрезки АС1, ВD1, СА1, DВ1.
Часто выделяют какие-нибудь две противоположные грани и называют их основаниями, а остальные грани – боковыми гранями параллелепипеда. Рёбра параллелепипеда, не принадлежащие основаниям, называются боковыми рёбрами.
 Если в качестве оснований параллелепипеда АВСDА1В1С1D1 выбрать грани АВСD и А1В1С1D1, то боковыми гранями будут параллелограммы АВВ1А1, ВСС1В1, СDD1С1, DА А1D1, а боковыми рёбрами отрезки АА1, ВВ1, СС1 и DD1.
Если в качестве оснований параллелепипеда АВСDА1В1С1D1 выбрать грани АВСD и А1В1С1D1, то боковыми гранями будут параллелограммы АВВ1А1, ВСС1В1, СDD1С1, DА А1D1, а боковыми рёбрами отрезки АА1, ВВ1, СС1 и DD1.
Упражнения:
1. В тетраэдре DАВС точки М, N, Q, Р – середины отрезков ВD, DС, АС, АВ. Найти периметр четырехугольника МNQР, если АD = 12 см, ВС = 14 см.
Дата добавления: 2016-05-11; просмотров: 1671;
