Укажите на модели куба несколько пар его ребер, лежащих на скрещивающихся прямых.
2. Через вершину А ромба АВСD проведена прямая а, параллельная диагонали ВD, а через вершину С – прямая b, не лежащая в плоскости ромба. Докажите, что прямые а и СD пересекаются, прямые а и b скрещиваются.
3. Дано: a · b,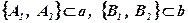 
. Доказать: А1В1 · А2В2 , А1В2 · А2В1.
3. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ
ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМОЙ И ПЛОСКОСТИ
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ
В пространстве рассматриваются три случая возможного расположения прямой и плоскости, вытекающие из аксиомы:
I3. Прямая, проходящая через две любые точки плоскости, лежит в этой плоскости.
Прямая лежит в плоскости (Рис. 1.);
Из аксиомы I3следует, что если прямая не лежит в плоскости, то она имеет с ней не более одной (одну или ни одной) общей точки.
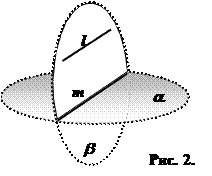
Прямая и плоскость пересекаются (Рис. 2.);
3. 
Прямая и плоскость не имеют общих точек (Рис. 3.).
Определение: Прямая и плоскость называются пересекающимися, если прямая и плоскость имеют одну общую точку (Рис. 2.)
Определение: Прямая и плоскость называются параллельными, если прямая и плоскость не имеют общих точек или когда прямая лежит в плоскости. (Рис. 3, 1.)
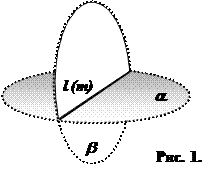
Теорема: (вспомогательная) Если плоскости a и b пересекаются и прямая l,принадлежащая плоскости b, параллельна плоскости a, то прямая l параллельна прямой, являющейся пересечением плоскостей a и b .
Дано: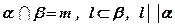 
.
Доказать: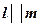 
Доказательство:
(Выполнить самостоятельно, рассматривая два случая: прямая l параллельна плоскости a, то есть прямая l лежит в плоскости a (Рис. 1.) или прямая l не имеет с плоскостью a общих точек (Рис. 2.))
 | |||
 | |||
Дата добавления: 2016-05-11; просмотров: 3420;