Адаптивное управление по заданной модели
Наиболее легко реализуется адаптивное управление по заданной модели. Идея этого метода основана на выборе соответствующей заданной модели и алгоритма адаптации, по которым изменяются коэффициенты передач обратных связей на двигатели в реальной системе. Алгритм адаптации проводится на основе информации об ошибках между выходами заданной модели и выходами реальной системы. Общая блок-схема адаптивного управления системой по заданной модели приведена на рис. 18.2.
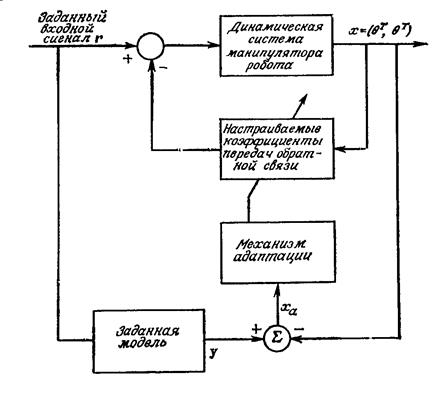
Рисунок 18.2.Общая блок-схема адаптивного управления системой
по заданной модели
В качестве заданной модели для каждой степени свободы манипулятора робота выбирается линейное дифференциальное уравнение второго порядка, не зависящее от времени. Манипулятор управляется путем настройки коэффициентов передачи обратной связи по положению и по скорости при отслеживании модели таким образом, чтобы его рабочие характеристики при замкнутом управлении совпадали с желаемыми рабочими характеристиками заданной модели. В результате такая схема адаптивного управления требует небольшого объема вычислений, которые могут выполняться с помощью недорогих микропроцессоров. Этот алгоритм адаптивного управления не требует ни сложных математических моделей динамической системы, ни предварительного знания внешних воздействий, таких, как величина нагрузки и др. Адаптивная схема, построенная по заданной модели, стабильно функционирует в широком диапазоне движений и нагрузок.
После определения вектора 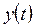 , описывающего динамику заданной модели, и вектора
, описывающего динамику заданной модели, и вектора 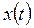 , описывающего динамику манипулятора, i-е сочленение заданной модели может быть описана следующим образом:
, описывающего динамику манипулятора, i-е сочленение заданной модели может быть описана следующим образом:
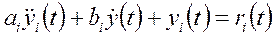 . (18-9)
. (18-9)
Коэффициенты 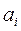 и
и 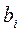 определяются из частоты собственных колебаний
определяются из частоты собственных колебаний 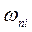 и коэффициента демпфирования
и коэффициента демпфирования 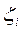 линейной системы второго порядка:
линейной системы второго порядка:
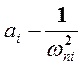 и
и 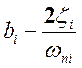 . (18-10)
. (18-10)
Учитывая, что членами высоких порядков можно пренебречь, уравнение динамики манипулятора для i-го сочленения может быть записано в виде:
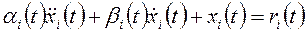 , (18-11)
, (18-11)
где 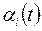 и
и 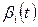 - медленно изменяющиеся во времени параметры системы.
- медленно изменяющиеся во времени параметры системы.
Дата добавления: 2016-05-25; просмотров: 1390;
