Адаптивное управление по возмущению
Адаптивное управление по возмущению отличается от других методов управления тем, что в нем учитываются все силы взаимодействия между различными сочленениями. Оптимальное управление базируется на линеаризованных уравнениях движения в окрестности номинальной траектории. Управляемая система характеризуется наличием прямой и обратной связей, которые могут быть рассчитаны отдельно и одновременно.
Прямая связь формирует номинальные моменты для компенсации всех сил взаимодействия между различными сочленениями при движении вдоль заданной траектории с помощью уравнений Ньютона-Эйлера, используемых в обратной задаче динамики манипулятора.
Обратная связь формирует моменты по возмущениям, которые уменьшают ошибки манипулятора по положению и по скорости до нуля вдоль заданной траектории.
При управлении линеаризованной возмущенной системой вдоль заданной траектории используется одношаговый оптимальный закон управления. Для получения необходимого управляющего воздействия параметры и коэффициенты передачи обратной связи пересчитываются и настраиваются в каждый дискретный период времени. Такой метод адаптивного управления позволяет свести задачу управления манипулятором от номинального управления к управлению линейной системой вдоль заданной траектории. В такой постановке задача управления формулируется как нахождение закона управления по обратной связи 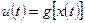 , такого, что замкнутая система управления
, такого, что замкнутая система управления 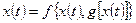 асимптотически устойчива и описывает максимально приближенную к желаемой траекторию в широком диапазоне нагрузок в каждый момент времени.
асимптотически устойчива и описывает максимально приближенную к желаемой траекторию в широком диапазоне нагрузок в каждый момент времени.
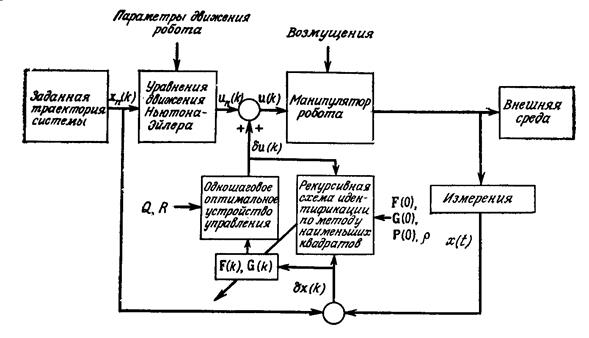
Рисунок 19.1. Адаптивное управление по возмущению
Рекурсивный алгоритм определения параметров по методу наименьших квадратов находится путем минимизации экспоненциального критерия ошибки, в котором учитывается квадрат ошибки последних измерений в виде:
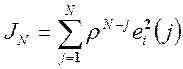 , (19-1)
, (19-1)
где вектор ошибки определяется выражением:
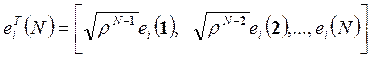 , (19-2)
, (19-2)
а 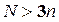 - число измерений, используемых для оценки параметров
- число измерений, используемых для оценки параметров 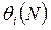 .
.
Оптимальное управление, минимизирующее функционал ошибки, описывается выражением:
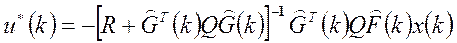 , (19-3)
, (19-3)
где 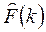 и
и 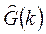 - параметры системы, полученные с помощью алгоритма идентификации в k-й дискретный момент времени.
- параметры системы, полученные с помощью алгоритма идентификации в k-й дискретный момент времени.
Весовой коэффициент настраивается для каждого вектора i-го параметра 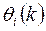 .
.
Дата добавления: 2016-05-25; просмотров: 794;
