Виды уравнений прямой и плоскости в декартовой системе координат
Общее уравнение прямой на плоскости
Определение. Любая прямая на плоскости может быть задана уравнением первого порядка
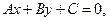
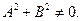 Это уравнение называют общим уравнением прямой.
Это уравнение называют общим уравнением прямой.
В зависимости от значений постоянных 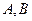 и
и 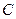 возможны следующие частные случаи:
возможны следующие частные случаи:
- 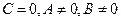 – прямая проходит через начало координат;
– прямая проходит через начало координат;
- 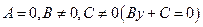 - прямая параллельна оси
- прямая параллельна оси 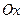 ;
;
- 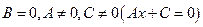 – прямая параллельна оси
– прямая параллельна оси 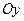 ;
;
- 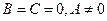 – прямая совпадает с осью
– прямая совпадает с осью 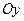 ;
;
- 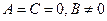 – прямая совпадает с осью
– прямая совпадает с осью 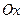 .
.
Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.
Уравнение прямой по точке и нормальному вектору
В декартовой прямоугольной системе координат вектор с координатами 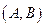 перпендикулярен прямой, заданной уравнением
перпендикулярен прямой, заданной уравнением 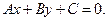 Он называется нормальным вектором прямой.
Он называется нормальным вектором прямой.
Пример. Найти уравнение прямой, проходящей через точку 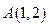 перпендикулярно вектору
перпендикулярно вектору 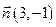 .
.
Для 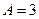 и
и 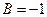 уравнение прямой примет вид:
уравнение прямой примет вид: 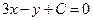 . Для нахождения коэффициента С подставим в полученное выражение координаты заданной точки А. Получаем
. Для нахождения коэффициента С подставим в полученное выражение координаты заданной точки А. Получаем 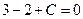 . Следовательно
. Следовательно 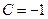 . Искомое уравнение запишется в виде
. Искомое уравнение запишется в виде 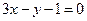 .
.
Дата добавления: 2016-05-05; просмотров: 945;
