Общее уравнения прямой в пространстве
Уравнение прямой можно рассматривать как уравнение линии пересечения двух плоскостей. Плоскость в векторной форме задаётся уравнением
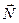 ×
× 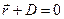 ,
,
где 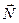 - нормальный вектор плоскости;
- нормальный вектор плоскости;  - радиус- вектор произвольной точки плоскости.
- радиус- вектор произвольной точки плоскости.
Пусть в пространстве заданы две плоскости: 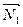 ×
× 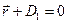 и
и 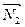 ×
× 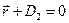 , нормальные векторы которых имеют координаты:
, нормальные векторы которых имеют координаты: 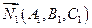 ,
,  , а
, а 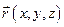 - радиус- вектор произвольной точки плоскости. Тогда общее уравнение прямой в векторной форме имеет вид:
- радиус- вектор произвольной точки плоскости. Тогда общее уравнение прямой в векторной форме имеет вид:
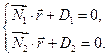
Общее уравнение прямой в координатной форме имеет вид:
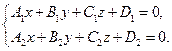
Приведём уравнение прямой в общем виде к каноническому виду.
Для этого найдём координаты произвольной точки прямой и числа 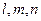 . При этом направляющий вектор прямой находится как векторное произведение векторов нормали к заданным плоскостям
. При этом направляющий вектор прямой находится как векторное произведение векторов нормали к заданным плоскостям
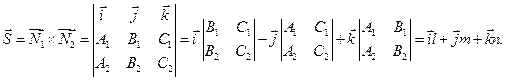
Пример. Найти каноническое уравнение прямой, если прямая задана в виде:
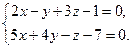
Для нахождения точки 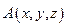 лежащей на прямой, положим
лежащей на прямой, положим 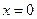 . Тогда
. Тогда
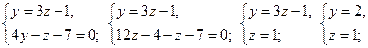 , т.е.
, т.е.  .
.
Находим компоненты направляющего вектора прямой

Каноническое уравнение прямой примет вид
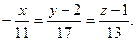
Основные задачи аналитической геометрии на плоскости и в пространстве
Дата добавления: 2016-05-05; просмотров: 573;
