Анализ общего качества уравнения регрессии.

Коэффициент детерминации R²

После проверки точности и статистической значимости каждого коэффициента регрессионной модели обычно проводится анализ общего качества уравнения модели, которое оценивается по тому, как хорошо эмпирическое уравнение регрессии согласуется со статистическими данными. Другими словами, необходимо оценить, насколько широко рассеяны точки наблюдений по их совокупности относительно линии регрессии (линии модели). Поэтому представляется естественным вывод о том, что проверку общего качества регрессионной модели следует проводить на основе дисперсионного анализа, сравнивая дисперсии модельных и реальных значений исследуемой переменной Y.

Рассмотрим для определенного набора наблюдений n дисперсию D_n(y), которая характеризует разброс значений y_i вокруг среднего значения. Из дисперсионного анализа следует, что эту дисперсию можно разбить на две части: объясняемую уравнением регрессии и не объясняемую (т. е. связанную со случайными отклонениями e_i). Тогда выполняется следующее соотношение:

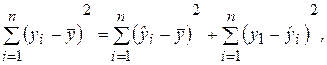(2.27)

где 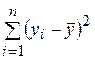– общая сумма квадратов отклонений зависимой переменной Y от среднего значения;

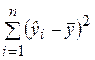– сумма квадратов, объясняемая уравнением регрессии;

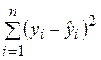– необъясненная (остаточная) сумма квадратов. Напомним, что 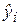определяется как 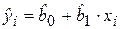, а .

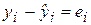Разделив выражение (2.27) на его левую часть, получим формулу для оценки характеристики, которая обозначается как R² и называется коэффициентом детерминации:

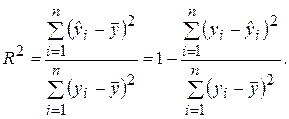(2.28)

Коэффициент детерминации R² является мерой качества уравнения регрессионной модели и определяет долю дисперсии (разброса), объясняемую регрессией Y на Х, в общей дисперсии зависимой переменной Y.

Из проведенных рассуждений следует, что R² принимает значения между 0 и 1 (0 £ R² £ 1). Чем ближе R² к единице, тем теснее линейная связь между Х и Y (экспериментальные точки теснее примыкают к линии регрессии). Чем ближе R² к нулю, тем такая связь слабее. Если R² = 0, то дисперсия зависимой переменной полностью обусловлена воздействием неучтенных факторов и линия регрессии (модели) должна быть параллельна оси абсцисс (Y = ).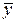

Например, если для построенной модели R² = 0,7, то согласно (2.28) можно утверждать, что поведение зависимой переменной (результативного признака) Y на 70 % объясняется влиянием фактора Х и на 30 % обусловлено влиянием неучтенных факторов. Доля влияния неучтенных факторов связана со случайными отклонениями e_i и определяется отношением 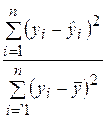, характеризующим долю разброса зависимой переменной, не объясняемую линейной регрессией Y на Х.

Естественно, что для исследуемого объекта наиболее качественной будет считаться модель с наибольшим значением коэффициента детерминации R².

Заметим, что коэффициент детерминации имеет смысл рассматривать только при наличии параметра 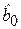(свободного члена) в уравнении регрессионной модели.

Таким образом, коэффициент детерминации R² определяет степень тесноты статистической связи между Y и Х. Но об этом же говорит выборочный коэффициент корреляции r_xy. Рассматривая эти характеристики, можно установить, что в случае парной линейной регрессионной модели коэффициент детерминации равен квадрату коэффициента корреляции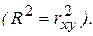

Действительно, учитывая (2.13),

.

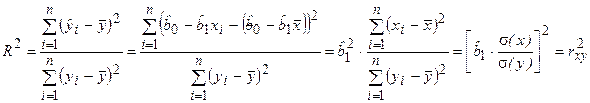Естественно, возникает вопрос, какое значение R² можно считать удовлетворительным. Ответ на этот вопрос может быть неоднозначным, особенно в случае множественной регрессионной модели и зависит от объема выборки n и постановки задачи, вытекающей из предмодельного анализа.

Более точно проверить значимость уравнения регрессии, т. е. установить, соответствует ли построенная модель реальным данным и достаточно ли включенных в уравнение объясняющих переменных для описания зависимой переменной, позволяет F-тест, который проводится по схеме статистической проверки гипотез. Тестируется гипотеза Н₀ о статистической незначимости уравнения регрессии.

Рассмотрим «объясненную» и «необъясненную» дисперсии: 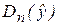и D_n(e). Отношение этих дисперсий, рассчитанное на одну степень свободы, имеет F-распределение (F-статистику), фактически наблюдаемое значение которой для парной регрессии определяется формулой

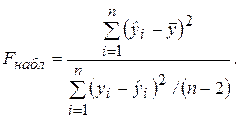(2.29)

Учитывая смысл дисперсий 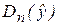и D_n(e), можно считать, что значение F_набл показывает, в какой мере уравнение регрессии лучше оценивает значение зависимой переменной по сравнению с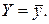

Согласно схеме статистической проверки гипотез, гипотеза Н₀ отклоняется, т. е. признается статистическая значимость и надежность уравнения регрессии на заданном уровне α, если F_набл превосходит критическое (табличное) значение F-статистики Фишера (F_набл > F_кр = F_α, 1, n - 2). Если F_набл < F_кр, то гипотеза Н₀ принимается и признается статистическая незначимость, ненадежность регрессионной модели.

Сравнивая формулы (2.28) и (2.29), критерий значимости можно записать в виде:

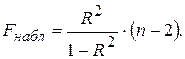(2.30)

Выражение (2.30) обычно используется на практике для оценки значимости, если известен коэффициент детерминации R². В этом случае гипотеза Н₀ о статистической незначимости регрессионной модели заменяется эквивалентной гипотезой о статистической незначимости R².

Для парной регрессионной модели способы проверки значимости коэффициента 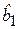с использованием t-критерия (t-тест) и уравнения регрессии (показателя тесноты связи R²) с использованием F-критерия равносильны, поскольку эти критерии связаны соотношением F = t².

Наряду с коэффициентом детерминации R² для оценки качества парной регрессионной модели можно использовать характеристику, называемую средней ошибкой аппроксимации :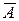

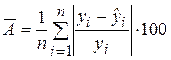%. (2.31)

Средняя ошибка аппроксимации определяет среднее относительное отклонение расчетных данных (оцененных по уравнению модели) от фактических. 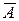является безразмерной величиной и обычно выражается в процентах. Принято считать, что качество модели считается удовлетворительным, если средняя ошибка аппроксимации не превышает 8-9 %.

Пример 2.3.Проверить общее качество и статистическую значимость уравнения регрессии для модели, построенной в примере 2.1.

Оценку качества построенной модели дают коэффициент детерминации R² и средняя ошибка аппроксимации .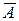

Вычислим коэффициент детерминации, воспользовавшись данными табл. 2.1.

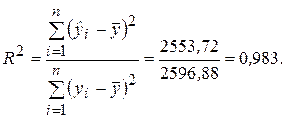
Величина коэффициента детерминации показывает, что поведение результативного признака (недельного потребления) Y на 98,3 % объясняется влиянием фактора Х (изменением недельного дохода), а остальные 1,7 % составляют долю необъясненной вариации, происходящей под действием прочих (неучтенных) факторов.

Расчет средней ошибки аппроксимации представлен в последнем столбце табл. 2.1.

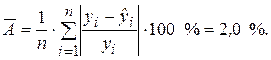
Рассчитанные значения коэффициента детерминации и средней ошибки аппроксимации свидетельствуют о достаточно высоком общем качестве построенной модели.

Проверим статистическую значимость уравнения регрессионной модели с помощью F-теста. Расчетное (наблюдаемое) значение F-статистики Фишера вычисляется по формуле:

.

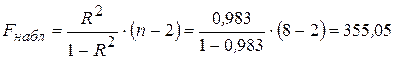Табличное значение F-статистики при уровне значимости α = 0,01 и числе степеней свободы ν = n – 2 будет составлять 13,75 (F_кр = 13,75).

Так как F_набл > F_кр (355,05 > 13,75), то нулевая гипотеза Н₀ отклоняется и уравнение регрессионной модели признается статистически значимым и весьма надежным, поскольку наблюдаемое значение F-статистики превосходит табличное значение критерия более чем в 25 раз.