Прогнозирование в регрессионных моделях

Одной из центральных задач эконометрики, имеющей большое практическое значение, является прогнозирование значений зависимой переменной при определенных значениях объясняющих (факторных) переменных с использованием построенной регрессионной модели.

В общем случае прогнозирование представляет собой задачу оценки зависимой переменной Y для некоторого набора объясняющих переменных, не входящих в область наблюдаемых статистических данных.

Точечное прогнозирование наиболее наглядно представляется в случае парной линейной регрессии, где возможна графическая экстраполяция (продолжение) линии модели до Х = х_р (рис. 2.3). Если наблюдаемые данные имеют временную структуру (временные ряды), то графическая экстраполяция показывает состояние системы в будущем.

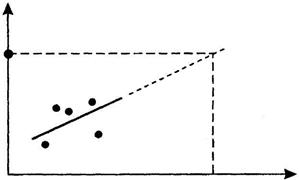
Рис. 2.3.

Основным аспектом проблемы прогнозирования является точность прогноза, которая определяется с помощью интервальных оценок зависимой переменной для линейной регрессии.

Прогнозирование среднего значения. Пусть построена парная регрессионная модель 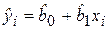, на основе которой необходимо предсказать условное математическое ожидание M_x(Y) при Х = х_р. В данном случае значение 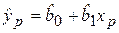будет являться выборочной оценкой M_x(Y).

С помощью интервальных оценок, построенных с заданной надежностью (1 – α), для конкретного значения х_р мы можем оценить величину отклонения модельного среднего значения (групповой средней) 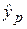от соответствующего математического ожидания.

Для построения доверительного интервала рассчитаем оценку дисперсии .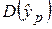

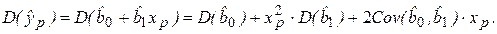(2.32)

Учитывая, что

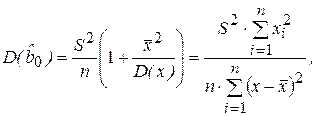(2.33)

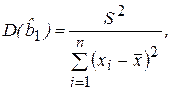(2.34)

(2.35)

где 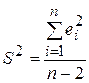является несмещенной оценкой теоретической дисперсии случайных отклонений 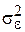, получим:

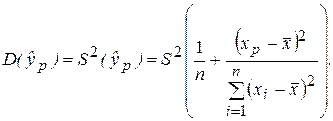(2.36)

Из положений регрессионного анализа следует, что СВ 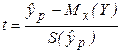имеет t-распределение (статистику) Стьюдента с ν = n – 2 степенями свободы. Тогда, зная 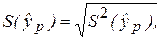можно построить доверительный интервал для условного математического ожидания (среднего значения) Y при Х = х_р

(2.37)

соответствующий требуемому уровню значимости α.

Прогнозирование индивидуальных значений зависимой переменной. Построенная доверительная область для М_х(Y) определяет возможное положение линии модели. Для практических применений более важным моментом является знание допустимых границ (ошибок прогноза) интересующего нас конкретного значения y₀. Предсказанное по уравнению регрессионной модели значение 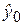составляет 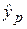при Х = х_р.

При определении доверительного интервала для индивидуальных значений y₀ зависимой переменной, которые отклоняются от средней, необходимо учитывать еще один источник дисперсии – рассеяние вокруг линии регрессионной модели, которое определяется величиной S². Включив в (2.36) величину S² в качестве слагаемого, получим оценку дисперсии индивидуальных значений y₀

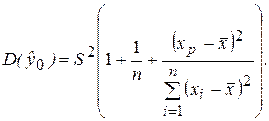(2.38)

Тогда соответствующий доверительный интервал для прогнозов индивидуальных значений зависимой переменной будет определяться по формуле:

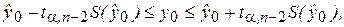(2.39)

где 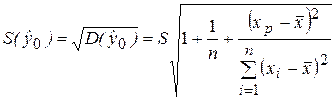представляет собой среднеквадратическую (среднюю стандартную) ошибку прогноза. Тогда предсказанное по уравнению модели значение у₀ можно записать как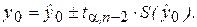

Построенный интервал определяет границы значений у₀, за пределами которых могут находиться не более 100 · a наблюдений при Х = х_р. Из формул (2.36) и (2.38) следует, что доверительные интервалы будут наиболее узкими при 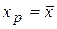и расширяются при удалении х_р от среднего значения (рис. 2.4).

Рис. 2.4.

С ростом числа наблюдений n доверительные интервалы сужаются (точность прогноза возрастает).

Пример 2.4.С использованием парной регрессионной модели (пример 2.1.) определить прогнозное значение потребления 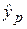при доходе х_р = 270 у.е. и оценить точность прогноза.

Прогнозное значение потребления 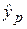определим, подставляя в уравнение регрессии Х = х_р:

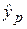= 31,845 + 0,390 · 270 = 137,11 у.е.

Для оценки точности прогноза вычислим среднюю стандартную ошибку по формуле:

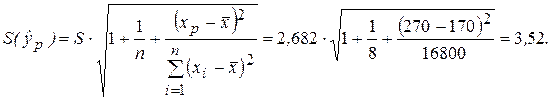
Здесь 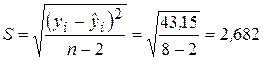– стандартная ошибка регрессионной модели. Расчеты проводим с использованием данных табл. 2.1.

Построим доверительный интервал для y_p, задавая уровень значимости α = 0,05. В соответствии с формулой (2.39) имеем:

137,11 - 2,45 · 3,52 £ y_p £ 137,11 + 2,45 · 3,52.

Таким образом, с вероятностью 0,95 можно утверждать, что уровень потребления при прогнозном значении дохода х_p = 270 у.е. будет находиться в интервале от 128,49 до 145,73 у.е.

Вопросы и упражнения для самопроверки

1. Сформулируйте наиболее общие задачи, решаемые методами регрессионного анализа в экономике.

2. Назовите основные причины присутствия в регрессионной модели случайного отклонения.

3. В чем сущность метода наименьших квадратов (МНК)?

4. Дайте общую интерпретацию коэффициентов (параметров) эмпирического уравнения парной линейной регрессионной модели.

5. Перечислите предпосылки (МНК). Каковы последствия их выполнимости либо невыполнимости?

6. Как определяются стандартные ошибки регрессионной модели и коэффициентов уравнения регрессии?

7. Объясните суть коэффициента детерминации и средней ошибки аппроксимации.

8. Опишите схему проверки статистической значимости коэффициентов регрессии и уравнения модели в целом.

9. Как определяются интервальные оценки коэффициентов регрессии?

10. В чем заключается сущность прогнозирования экономических показателей в регрессионных моделях?

11. Приведите схему определения оценок точности прогноза.

12. По 10 парам наблюдений получены следующие результаты:

; ;

;

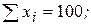
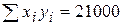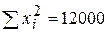С использованием МНК оцените коэффициенты уравнения регрессии Y на Х.

Оцените выборочный коэффициент корреляции r_xy.

13. При исследовании корреляционной зависимости между ценой на нефть Х и индексом нефтяных компаний Y получены следующие данные:

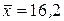(ден. ед), 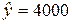(усл. ед), D(x) = 4, Cov(X, Y) = 40.

Необходимо: а) составить уравнение регрессии Y на Х; б) используя уравнение регрессии, найти среднее значение индекса при цене на нефть 16,5 ден. ед.

14. В таблице приведены статистические данные об объеме спроса Y и цене Х на некоторый товар:

а) постройте корреляционное поле и по расположению точек сделайте предположение о виде зависимости между Х и Y;

б) по МНК постройте регрессионную модель зависимости спроса от цены и проведите общую интерпретацию построенной модели. Изобразите линию модели на корреляционном поле;

в) проверьте общее качество регрессионной модели, рассчитав значения коэффициента детерминации и средней ошибки аппроксимации;

г) рассчитайте характеристики точности оценок коэффициентов регрессии (параметров модели) и оцените статистическую значимость коэффициентов;

д) проведите F-тест, сделайте вывод о статистической значимости уравнения регрессионной модели;

е) оцените прогнозное значение спроса при цене Х_р = 12 руб. и постройте 95%-й доверительный интервал для данного прогноза.