Оценка параметров регрессионной модели
Для нахождения оценок параметров bj множественной линейной регрессионной модели (коэффициентов  эмпирического уравнения регрессии) используется метод наименьших квадратов (МНК). Суть МНК заключается в минимизации суммы квадратов отклонений наблюдаемых выборочных значений yi зависимой переменной Y от их модельных оценок
эмпирического уравнения регрессии) используется метод наименьших квадратов (МНК). Суть МНК заключается в минимизации суммы квадратов отклонений наблюдаемых выборочных значений yi зависимой переменной Y от их модельных оценок  . Отклонение еi, соответствующее уравнению регрессии в i-м наблюдении (i = 1, 2, …, n), рассчитывается по формуле:
. Отклонение еi, соответствующее уравнению регрессии в i-м наблюдении (i = 1, 2, …, n), рассчитывается по формуле:
 . (3.7)
. (3.7)
Тогда для нахождения коэффициентов 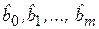 по МНК минимизируется следующая функция m + 1 переменных:
по МНК минимизируется следующая функция m + 1 переменных:
 . (3.8)
. (3.8)
Необходимым условием минимума функции G является равенство нулю всех ее частных производных по  Частные производные квадратичной функции (3.8) являются линейными функциями относительно параметров:
Частные производные квадратичной функции (3.8) являются линейными функциями относительно параметров:
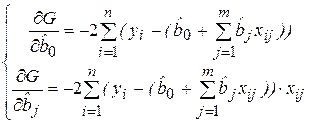 . (3.9)
. (3.9)
Приравнивая (3.9) к нулю, получаем систему m + 1 линейных нормальных уравнений с m + 1 неизвестными для определения параметров модели:
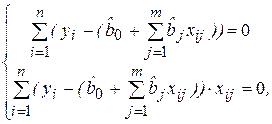 (3.10)
(3.10)
где j = 1, 2, …, m – определяет набор регрессоров.
Следует заметить, что включение в модель новых объясняющих переменных усложняет расчет коэффициентов множественной линейной регрессии путем решения системы (3.10) по сравнению с парной моделью. Система из трех уравнений, соответствующая модели с двумя объясняющими переменными 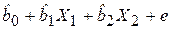 , может быть легко решена методом определителей. Однако в общем виде решение системы (3.10) и анализ множественной регрессионной модели наиболее целесообразно проводить в векторно-матричной форме.
, может быть легко решена методом определителей. Однако в общем виде решение системы (3.10) и анализ множественной регрессионной модели наиболее целесообразно проводить в векторно-матричной форме.
Тогда, вводя матричные обозначения, запишем:

 ,
,  ,
, 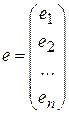 .
.
Здесь Y – n-мерный вектор-столбец наблюдений зависимой переменной; Х – матрица размерности n · (m + 1) значений объясняющих переменных xij, в которой единица соответствует переменной при свободном члене  ;
; 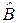 – вектор-столбец размерности m + 1 оценок параметров модели (коэффициентов уравнения регрессии); е – вектор-столбец размерности n отклонений выборочных (реальных) значений yi зависимой переменной, от значений оценок
– вектор-столбец размерности m + 1 оценок параметров модели (коэффициентов уравнения регрессии); е – вектор-столбец размерности n отклонений выборочных (реальных) значений yi зависимой переменной, от значений оценок  , получаемых по уравнению регрессии.
, получаемых по уравнению регрессии.
В матричной форме модель (3.1) примет вид:
Y = XB + e. (3.11)
Оценкой этой модели по выборочным данным является уравнение (эмпирическая модель)
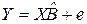 . (3.12)
. (3.12)
Предпосылки МНК (см. раздел 2.4.1.) в матричной форме можно записать следующим образом:
1. M(e) = 0; 2. D(e) = σ2I. 3. Матрица ковариаций V(e) = M(e · eT) = σ2E,
где 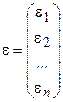 – вектор-столбец случайных отклонений (ошибок);
– вектор-столбец случайных отклонений (ошибок);
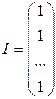 – (n · 1) вектор;
– (n · 1) вектор;
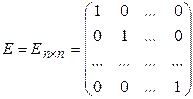 – единичная матрица;
– единичная матрица;
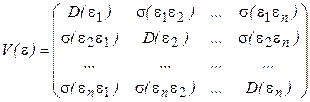 – матрица ковариаций или ковариационная матрица вектора случайных отклонений, которая является многомерным аналогом дисперсии одной переменной и в которой, если предпосылка о некоррелированности отклонений ei и ej выполняется, все элементы, не лежащие на главной диагонали, равны нулю, а элементы главной диагонали равны одной и той же дисперсии D(ei) = σ2; 4. e – нормально распределенный случайный вектор, т. е. e ~ N(0, σ2Е); 5. r(X) = m + 1 > n – детерминированная матрица объясняющих переменных (регрессоров) имеет ранг r, равный числу определяемых параметров модели m + 1, кроме того, число имеющихся наблюдений каждой из объясняющих переменных и зависимой переменной превосходит ранг матрицы Х.
– матрица ковариаций или ковариационная матрица вектора случайных отклонений, которая является многомерным аналогом дисперсии одной переменной и в которой, если предпосылка о некоррелированности отклонений ei и ej выполняется, все элементы, не лежащие на главной диагонали, равны нулю, а элементы главной диагонали равны одной и той же дисперсии D(ei) = σ2; 4. e – нормально распределенный случайный вектор, т. е. e ~ N(0, σ2Е); 5. r(X) = m + 1 > n – детерминированная матрица объясняющих переменных (регрессоров) имеет ранг r, равный числу определяемых параметров модели m + 1, кроме того, число имеющихся наблюдений каждой из объясняющих переменных и зависимой переменной превосходит ранг матрицы Х.
Выполнение пятой предпосылки означает линейную независимость объясняющих переменных (линейную независимость столбцов матрицы Х), т. е. отсутствие функциональной мультиколлинеарности.
Наша задача заключается в нахождении вектора оценок 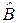 по МНК, который, при выполнении предпосылок 1–5, обладает наименьшим рассеянием относительно параметра B.
по МНК, который, при выполнении предпосылок 1–5, обладает наименьшим рассеянием относительно параметра B.
Воспользовавшись известными соотношениями матричной алгебры и правилами дифференцирования по векторному аргументу, получим необходимое условие минимума функции G (равенство нулю вектор-столбца частных производных 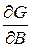 )
)
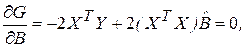 (3.13)
(3.13)
откуда вытекает система нормальных уравнений в матричной форме для определения вектора 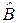
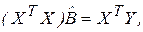 (3.14)
(3.14)
где ХТ – транспонированная матрица.
Решением уравнения (3.14) является вектор оценок:
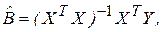 (3.15)
(3.15)
где (ХТХ)-1 – матрица, обратная ХТХ; ХТY – вектор-столбец свободных членов системы.
Найдем матрицы, входящие в матричное уравнение (3.14):
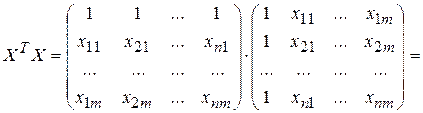
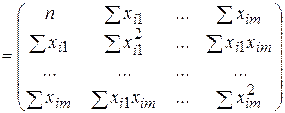 . (3.16)
. (3.16)
Матрица ХТХ образует симметричную матрицу сумм первых степеней, квадратов и попарных произведений n наблюдений объясняющих переменных.
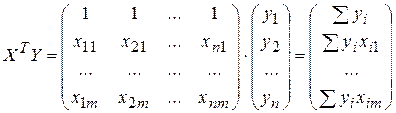 . (3.17)
. (3.17)
Матрица ХТХ представляет вектор-столбец произведений n наблюдений объясняющих и зависимой переменных.
Зная вектор коэффициентов множественной линейной регрессии 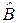 (3.15), находим оценку (групповую среднюю)
(3.15), находим оценку (групповую среднюю) 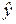 зависимой переменной Y при заданном векторе значений объясняющей (факторной) переменной
зависимой переменной Y при заданном векторе значений объясняющей (факторной) переменной 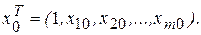
Пример 3.1. Для иллюстрации получим формулы для расчета коэффициентов парной регрессии 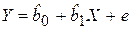 (m = 1), используя матричные обозначения.
(m = 1), используя матричные обозначения.
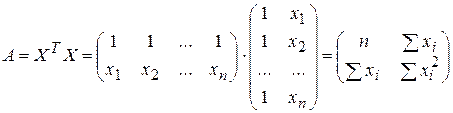
В соответствии с (3.17) определим матрицу А-1 = (ХТХ)-1 по формуле:
 ,
,
где detA – определитель матрицы ХТХ; A*– присоединенная матрица.
Для данного примера:
 .
.
 ,
, 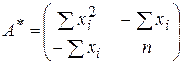 .
.
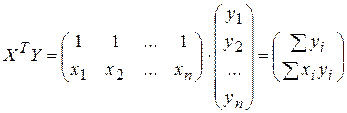 .
.
Тогда вектор оценок 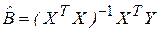 для частного случая m = 1 определяется как:
для частного случая m = 1 определяется как:
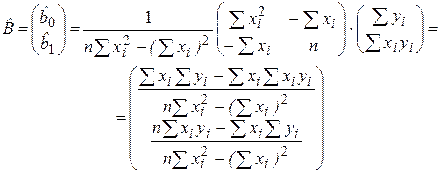 ,
,
откуда следуют формулы (2.11) для определения параметров парной регрессионной модели.
Дата добавления: 2016-06-02; просмотров: 1407;
