Метод наименьших квадратов

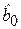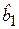Рассмотрим задачу аппроксимации набора наблюдений x_i, y_i (i = 1, 2, …, n) линейной функцией регрессии. Основной этап решения этой задачи состоит в определении по конкретной выборке пар значений (x_i, y_i) таких оценок и неизвестных параметров b₀ и b₁, чтобы построенная линия регрессии (эмпирическая линейная регрессионная модель) являлась «наилучшей» среди всех других прямых. Другими словами, построенная прямая (линия модели) 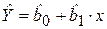(рис. 2.1) должна быть ближайшей к точкам наблюдений по их совокупности.

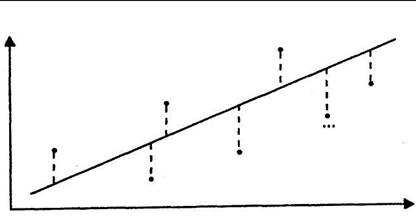
Рис. 2.1.

Мерой качества найденных оценок параметров могут служить определенные композиции отклонений е_i.

В качестве меры соответствия линии регрессии (модели) наблюдаемым значениям удобно рассматривать сумму квадратов отклонений 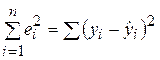, что дает возможность построить достаточно развитую статистическую теорию.

Метод определения оценок параметров линейной регрессионной модели (коэффициентов регрессии), заключающийся в минимизации суммы квадратов отклонений выборочных данных y_i от модельных (регрессионных) значений 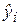, называется методом наименьших квадратов (МНК).

В случае парной линейной регрессии при использовании МНК минимизируется следующая функция двух параметров:

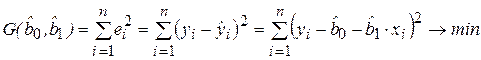. (2.8)

На основании необходимого условия существования минимума функции двух переменных (2.8) приравниваем к нулю ее частные производные по неизвестным параметрам 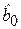и :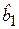

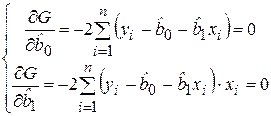. (2.9)

Раскрыв скобки и перегруппировав слагаемые, получим систему двух линейных уравнений для определения 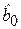и :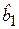

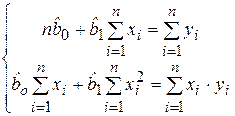. (2.10)

Разделив оба уравнения (2.10) на n и решая систему, найдем

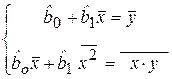
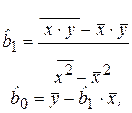, (2.11)

где соответствующие средние находятся по формулам:

Нетрудно заметить, что решение для 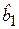можно записать в виде:

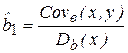, (2.12)

где Cov_в(x, y) – выборочная ковариация, а D_в(x) - выборочная дисперсия объясняющей переменной (фактора-аргумента) Х. Тогда, преобразуя (2.12), получим:

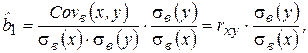(2.13)

где r_xy - выборочный коэффициент корреляции; 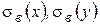– выборочные средние квадратические отклонения. Таким образом, зная коэффициент корреляции, можно легко найти коэффициент парной регрессии .

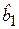Оценка 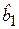называется выборочным коэффициентом регрессии (или просто коэффициентом регрессии) и обычно имеет достаточно ясный экономический смысл. В целом он показывает, на сколько единиц в среднем изменяется результирующая переменная Y при увеличении объясняющей переменной Х на одну единицу.

Резюмируя проведенные рассуждения, можно сделать следующие выводы:

1. Оценки параметров модели по МНК являются функциями от объема выборки n, что позволяет достаточно легко их рассчитывать.

2. Оценки по МНК являются точечными оценками теоретических коэффициентов регрессии.

3. Из формулы для определения параметра 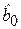следует, что эмпирическая прямая регрессии (линия модели) проходит через точку 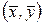; т. е. .

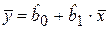4. Из первой формулы соотношения (2.9) следует, что сумма отклонений 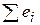, а также среднее значение 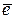равны нулю.

Для иллюстрации МНК рассмотрим следующий пример.

Пример 2.1. Приведены статистические данные недельного дохода (Х) и недельного потребления (Y) в у.е. для домашних хозяйств (см. таблицу).

Необходимо построить парную (однофакторную) регрессионную модель зависимости потребления от располагаемого дохода.

Для наглядности и предварительного анализа нанесем точки x_i, y_i (n = 8) на координатную плоскость и получим так называемое корреляционное поле или диаграмму рассеяния (рис. 2.2).

Рис. 2.2.

По характеру расположения точек на корреляционном поле можно предположить, что зависимость между Y и Х является линейной:

Для построения уравнения парной линейной регрессии по МНК составим вспомогательную табл. 2.1. Тогда, согласно МНК, имеем:

– оценка коэффициента регрессии;

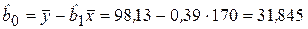– оценка свободного члена.

Для нахождения оценок параметров модели необходимы данные первых четырех столбцов таблицы. Остальные данные будут необходимы для последующего анализа качества построенной модели.

Таблица 2.1

xi	yi	xiyi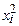
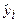
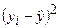
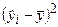
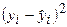
				70,83 78,63 86,43 94,23 102,02 109,82 117,62 125,42	791,02 328,52 66,02 66,02 3,52 141,02 478,52 722,27	744,84 380,02 136,81 15,20 15,20 136,81 380,02 744,84	0,69 1,87 12,76 17,86 4,10 0,03 5,67 0,17	0,0119 0,0171 0,0397 0,0470 0,0202 0,0016 0,0198 0.0033
Сумма:				-	2596,88	2553,72	43,15	0,1607
Средн.:	98,13			-	-		5,39	0,0201

Таким образом, построенная модель парной регрессии (уравнение регрессии) имеет вид:

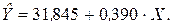
По этому уравнению рассчитаем модельные значения 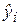и построим линию модели (рис. 2.2).

Графически задачу парной линейной регрессии можно представить следующим образом. В «облаке» точек x_i, y_i плоскости XY следует провести прямую так, чтобы совокупность всех отклонений отвечала условию МНК (2.8).

В нашем примере параметр модели 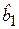можно трактовать как предельную склонность к потреблению. Фактически он показывает, на какую величину изменяется объем потребления при возрастании располагаемого дохода на одну единицу. Параметр 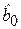, равный в данной модели 31,845 у.е., определяет среднюю прогнозируемую величину недельного потребления при отсутствии дохода (Х = 0), т. е. имеет смысл автономного потребления. Этот факт можно объяснить для отдельного домохозяйства как использование одолженных средств (постоянная величина долга) или накопленных сбережений. Следует заметить, что в большинстве ситуаций этот параметр не имеет содержательной экономической интерпретации. В любом случае значение свободного члена 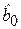определяет точку пересечения прямой с осью ординат и сдвиг линии модели вдоль оси Y.